Given a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
3MR2/32
5MR2/16
1MR2/64
none of these
The correct Answer is:C
Mass is cut disc m1=M4
Moment of inertia of original disc about axis 1:

I=14MR2
Moment of inertia of small disc about axis 1:
I'=14m1(R2)2+m1(R2)2
516m1R2=564MR2
Required moment of inertia
I−I'=14MR2−564MRS2=1164MR2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionObtain an expression for moment of inertia of a uniform circular disc about a diameter of the disc.
View Solution
Knowledge Check
- Question 1 - Select One
A small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
A0.4mB2.4cmC1.8cmD1.2cm - Question 2 - Select One
A small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
A0.4 cmB2.4 cmC1.8 cmD1.2 cm - Question 3 - Select One
A disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
Ar5Br4Cr2Dr3
A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
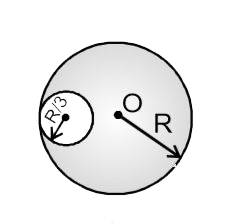 View Solution
View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe moment of inertia of a uniform semicircular disc of mass disc through the centre is
View Solution

