Given in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
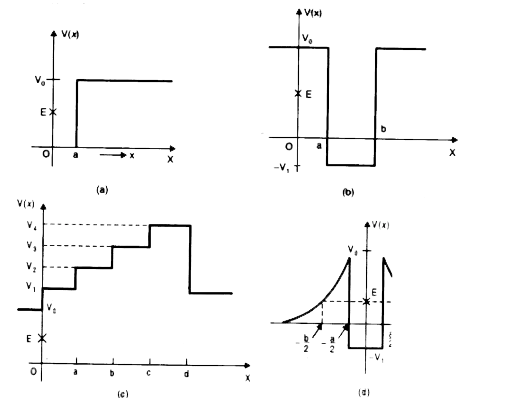
(a) For x>a ,
P.E > Total Energy
Hence K.E is negative which is not possible .
Therefore , particle cannot exist in the region .
In the region x<a , the minimum energy the particle can have is when it is at rest , that is its kinetic energy is zero . Also we see that the potential energy for this region is also zero . Thus , minimum total energy is zero .
Therefore particle cannot exist in this region .
(b ) For every region , the potential energy is greater than teh total energy and hence K.E is negative which is not possible , Hence , particle cannot be found in any region .
The minimu energy of the particle is V1 , when it is at x = 0
(c ) As the potential energy is lesser tha the total energy in the region a<x<b . Therefoore , the particle cannot exist in this region x<a and x>b .
The minimum energy of the aprticle is V1
(d) For −b2<x−a2anda2<x<b2, P.E >E ( total energy )
K.E is negative . the particle cannot be found in these regions . The minimum energy of the particle is −V1 .
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - NCERT FILE (NCERT Additional Exercise)
7 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - NCERT FILE (Exemplar Problems Objective Questions)
21 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Tough & Tricky (PROBLEMS)
15 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Given in fig are examples of some potential energy functions in one dimension. The total enrgy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

View SolutionThe total energy of a particle executing simple harmonic motion is
View Solution
Knowledge Check
In which case does the potential energy decrease ?
Aon compressing the springBon stretching a springCon moving a body against gravitational pullDon rising of an air bubble in waterThe total energy of particle executing SHM is proportional to
AdisplacementBfrequencyCvelocity at mean positionDsquare of amplitudeThe total energy of particle executing SHM is proportional to
AdisplacementBfrequencyCvelocity at mean positionDsquare of amplitude
A particle of mass m is executing SHM about its mean position. The total energy of the particle at given instant is
View SolutionThe total energy of particle performing SHM depend on : -
View SolutionA particle of mass m executing S.H.M. about its mean position. The total energy of the particle at given instant is
View SolutionThe kinetic energy of the particles is maximum in the case of ____.
View SolutionPotential energy of the particle performing S.H.M. is
View Solution
