Given that $\to A + \to B = \to C$ and that $\to C$ is perpendicular to $\to A$ Further if $∣ ∣ \to A ∣ ∣ = ∣ ∣ \to C ∣ ∣$ , then what is the angle between $\to A$ and $\to B$

A

$\frac{π}{4}$

B

$\frac{π}{2}$

C

$\frac{3 π}{4}$

D

$π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

(c ) from the figurer $B cos t h e r t a = C and B sin θ = A$

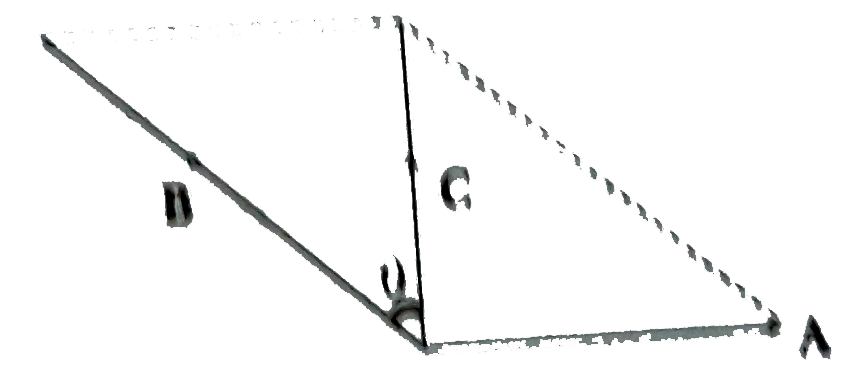
But A=C
$∴ B cos θ = B sin θ or θ = 45^{\circ}$
$∴$ Angle between A and B is $135^{\circ}$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Given that $\to A + \to B = \to C$ and that $\to C$ is perpendicular to $\to A$ Further if $∣ ∣ \to A ∣ ∣ = ∣ ∣ \to C ∣ ∣$ , then what is the angle between $\to A$ and $\to B$
A $\frac{π}{4} r a d$
B $\frac{3 π}{4} r a d$
C $\frac{5 π}{4} r a d$
D $\frac{7 π}{4} r a d$
Question 2 - Select One
If $\to A + \to B = \to C$ and $A + B = C$ , then the angle between $\to A$ and $\to B$ is :
A0
B $\frac{π}{4}$
C $\frac{π}{2}$
D $π$
Question 3 - Select One
If $\to a . \to b and \to c$ are unit vectors such that $\to a$ is perpendicular to the plane of $\to b, \to c$ and the angle between $\to b and \to c$ is $\frac{π}{3}$ . Then what is $∣ ∣ \to a + \to b + \to c ∣ ∣$ ?
AA) 1
BB) 2
CC) 3
DD) 4

DC PANDEY-BASIC MATHEMATICS-Exercise

Home
Ask Doubt
Profile