How do vibrations of a simple pendulum and motion of a ball over a watch glass illustrate the principle of energy conservation ?
To illustrate how the vibrations of a simple pendulum and the motion of a ball over a watch glass demonstrate the principle of energy conservation, we can break down the explanation into clear steps:
1. Understanding Energy Conservation:
- The principle of energy conservation states that the total energy in a closed system remains constant. Energy can neither be created nor destroyed; it can only change forms.
2. Analyzing the Simple Pendulum:
- Consider a simple pendulum that is displaced from its equilibrium position and then released. Initially, it has maximum potential energy (PE) at its highest point because it is at a height relative to its lowest point.
3. Energy Transformation in the Pendulum:
- As the pendulum swings downwards, its height decreases, leading to a decrease in potential energy. However, as it falls, it gains speed, which means its kinetic energy (KE) is increasing.
- At the lowest point of the swing, the pendulum has maximum kinetic energy and zero potential energy.
- As it swings back up, the kinetic energy decreases while the potential energy increases again, demonstrating that energy is being transformed between kinetic and potential forms, but the total mechanical energy (PE + KE) remains constant throughout the motion.
4. Examining the Ball on a Watch Glass:
- Now, consider a ball rolling over a watch glass. When the ball is at the highest point on the watch glass, it has maximum potential energy due to its height.
- As the ball rolls down, its height decreases, resulting in a decrease in potential energy and an increase in kinetic energy as it speeds up.
- At the lowest point of the watch glass, the ball has maximum kinetic energy and minimum potential energy.
- As it rolls back up, the kinetic energy decreases while potential energy increases, again illustrating the transformation of energy forms while keeping the total energy constant.
5. Conclusion:
- In both cases, the simple pendulum and the ball on the watch glass, we observe that energy is conserved. The total mechanical energy remains constant as it shifts between potential and kinetic forms, illustrating the principle of energy conservation.
- The principle of energy conservation states that the total energy in a closed system remains constant. Energy can neither be created nor destroyed; it can only change forms.
- Consider a simple pendulum that is displaced from its equilibrium position and then released. Initially, it has maximum potential energy (PE) at its highest point because it is at a height relative to its lowest point.
- As the pendulum swings downwards, its height decreases, leading to a decrease in potential energy. However, as it falls, it gains speed, which means its kinetic energy (KE) is increasing.
- At the lowest point of the swing, the pendulum has maximum kinetic energy and zero potential energy.
- As it swings back up, the kinetic energy decreases while the potential energy increases again, demonstrating that energy is being transformed between kinetic and potential forms, but the total mechanical energy (PE + KE) remains constant throughout the motion.
- Now, consider a ball rolling over a watch glass. When the ball is at the highest point on the watch glass, it has maximum potential energy due to its height.
- As the ball rolls down, its height decreases, resulting in a decrease in potential energy and an increase in kinetic energy as it speeds up.
- At the lowest point of the watch glass, the ball has maximum kinetic energy and minimum potential energy.
- As it rolls back up, the kinetic energy decreases while potential energy increases, again illustrating the transformation of energy forms while keeping the total energy constant.
- In both cases, the simple pendulum and the ball on the watch glass, we observe that energy is conserved. The total mechanical energy remains constant as it shifts between potential and kinetic forms, illustrating the principle of energy conservation.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Advanced Problems For Competitions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT EXERCISES WITH SOLUTIONS
30 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Short Answer Question
52 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
State and explain Lenz's law. Give one exmple to illustrate the law. How will you verify it experimentally ? Does it obey the principle of energy consevartion ?
View SolutionThe bob of a vibrating simple pendulum is made of ice. How will the period of swing will change when the ice starts melting?
View Solution
Knowledge Check
Statement 1 : Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.
Statement 2 : The principle of conservation of momentum holds true for all kinds of collisions.AStatement-1 is True, Statement-2 is True and Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True and Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.For a simple pendulum in simple harmonic motion, which of the following statements is/are correct?
1. The kinetic energy is maximum at the mean position.
2. The potential energy is maximum at the mean position.
3. Acceleration is maximum at the mean position. Select the correct answer using the code given below: Code:A1 onlyB2 onlyC1 and 3D2 and 3
In figue k=100Nm−1M=1kgandF=10N. a. Find the compression of the spring in the equilibrium position. b. A sharp blow by some xternal agent imparts a speed of 2ms−1 to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at ths instant. c. find the time period of the resulting simple harmonic motion. d. Find the ampitude. e. Write the potential energy of the spring when the block is at the left extreme. f. Write teh potential energy of the spring when teh block is at the right extreme.
The anwer of b, e, and f are different. Explain why this does not violate the principle of conservation of energy.
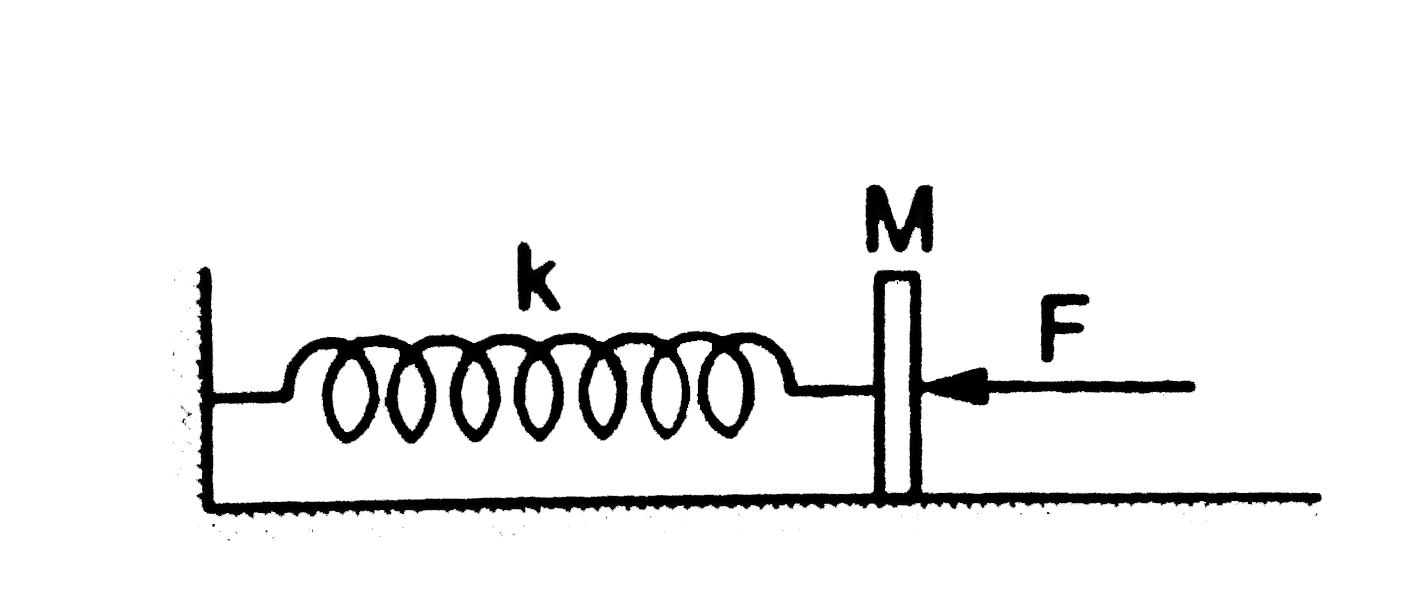
View SolutionIn figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View Solution(a) Derive an expression for the energy of a particle executing simple harmonic motion.
(b) The length of a simple pendulum in increased by 15%. What will be the percentage increase in time period ?
View SolutionDefine practical simple pendulum. Show that motion of bob of pendulum with small amplitude is linear S.H.M. Hence obtain an expression for its period. What are the factors on which its period depends ?
The total free surface energy of a liquid drop is π√2 times the surface tensin of the liquid. Calculate the diameter of the drop in S.I unit.
View SolutionConsider an excited hydrogen atom in state n moving with a velocity υ(υ<<c). It emits a photon in the direction of its motion and changes its state to a lower state m. Apply momentum and energy conservation principle to calculate the frequency v of the emitted radiation, compare this with the frequency v0 emitted if the atom were at rest.
View SolutionIn an experiment of simple pendulum, time period measured was 50s for 25 vibrations when the length of the simple pendulum was taken to be 100cm. If the lest count of stop watch is 0.1s and that of metre scale is 0.1cm, calculate the maximum possible percentage error in the measurement of value of g.
View Solution
