How does the orbital velocity of a satellite depend on the mass of the satellite ?
To determine how the orbital velocity of a satellite depends on the mass of the satellite, we can follow these steps:
Step 1: Understand the Forces Acting on the Satellite
A satellite in orbit experiences two main forces: gravitational force and centripetal force. The gravitational force acts as the centripetal force that keeps the satellite in its circular path.
Step 2: Write the Expression for Centripetal Force
The centripetal force required to keep a satellite of mass ms moving in a circular orbit of radius r with velocity v is given by:
Fc=msv2r
Step 3: Write the Expression for Gravitational Force
The gravitational force acting on the satellite due to the planet of mass M is given by Newton's law of gravitation:
Fg=GmsMr2
where G is the gravitational constant.
Step 4: Set the Centripetal Force Equal to the Gravitational Force
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal to each other:
msv2r=GmsMr2
Step 5: Cancel Out the Mass of the Satellite
We can simplify the equation by canceling ms from both sides (assuming ms≠0):
v2r=GMr2
Step 6: Solve for Orbital Velocity
Rearranging the equation to solve for v2:
v2=GMr
Taking the square root gives us the expression for orbital velocity v:
v=√GMr
Step 7: Analyze the Result
From the derived formula v=√GMr, we can see that the orbital velocity v depends on:
- The mass of the planet M
- The radius of the orbit r
Conclusion
The orbital velocity of a satellite is independent of the mass of the satellite itself. The mass of the satellite does not appear in the final expression for orbital velocity.
A satellite in orbit experiences two main forces: gravitational force and centripetal force. The gravitational force acts as the centripetal force that keeps the satellite in its circular path.
The centripetal force required to keep a satellite of mass ms moving in a circular orbit of radius r with velocity v is given by:
Fc=msv2r
The gravitational force acting on the satellite due to the planet of mass M is given by Newton's law of gravitation:
Fg=GmsMr2
where G is the gravitational constant.
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal to each other:
msv2r=GmsMr2
We can simplify the equation by canceling ms from both sides (assuming ms≠0):
v2r=GMr2
Rearranging the equation to solve for v2:
v2=GMr
Taking the square root gives us the expression for orbital velocity v:
v=√GMr
From the derived formula v=√GMr, we can see that the orbital velocity v depends on:
- The mass of the planet M
- The radius of the orbit r
The orbital velocity of a satellite is independent of the mass of the satellite itself. The mass of the satellite does not appear in the final expression for orbital velocity.
Topper's Solved these Questions
Similar Questions
The orbital velocity v of a satellite may depend on its mass m , the distane r from the centre of the earth and acceleration due to gravity g . Obtain an expression for its orbital velocity .
View SolutionDefine orbital velocity of a satellite. Derive expressions for the orbital velocity of a satellite. Show that the escape velocity of a body from the earth's surface is √2 times its velocity in a circular orbit just above the earth's surface.
View Solution
Knowledge Check
STATEMENT -1 : Time period of a satellite is inversely propertional to the square root of the mass of planet.
STATEMENT -2 : Self gravitational potential energy of earth is positive.
STATEMENT -3 : Orbital velocity of a satellite does depend upon the mass of planet.AT T TBT F FCT F TDF F FCritical velocity of satellite depends on ......... .
Aorbit of satelliteBmassCspeed of satelliteDnone of theseAssertion : The binding energy of a satellite does not depend upon the mass of the satellite.
Reason : Binding energy is the negative value of total energy of satellite.AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
Derive expression for the orbital velocity of a satellite and its time period. What is a geostationary satellite. Obtain the expression for the height of the geostationary satellite.
View SolutionOrbital velocity of a satellite around a planet is independent of the mass of the ____ but depends on the mass of the .
View SolutionOrbital velocity of a satellite depends on the ………..the planet around which the satellite revolves.
View SolutionObserve the following diagram and answer the questions:
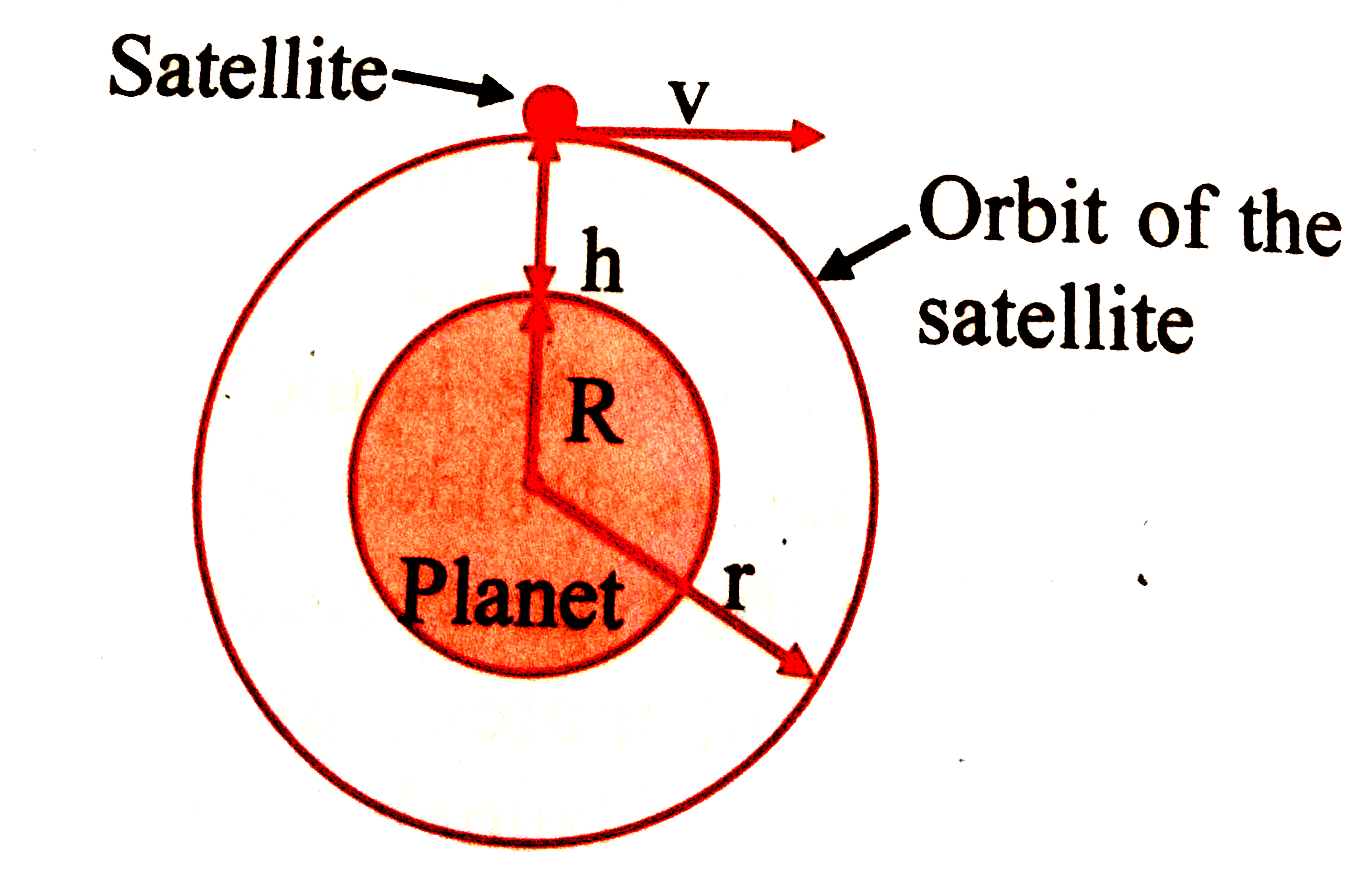
Derive the formula for that velocity of satellite assuming the mass of the planet M and mass of satellite as m .
View SolutionIf v0 be the orbital velocity of an articial satellite orbital velocity of the same satellite orbiting at an altitude equal to earth's radius is
View Solution
