How many minimum numbers of non zero vectors in different planes can be added to give zero resultant.
A
2
B
3
C
4
D
5
Video Solution
Text Solution
The correct Answer is:B
→F3=→F1+→F2
There should be minimum three coplanar vectors having different magnitude which should be added to give zero resultant
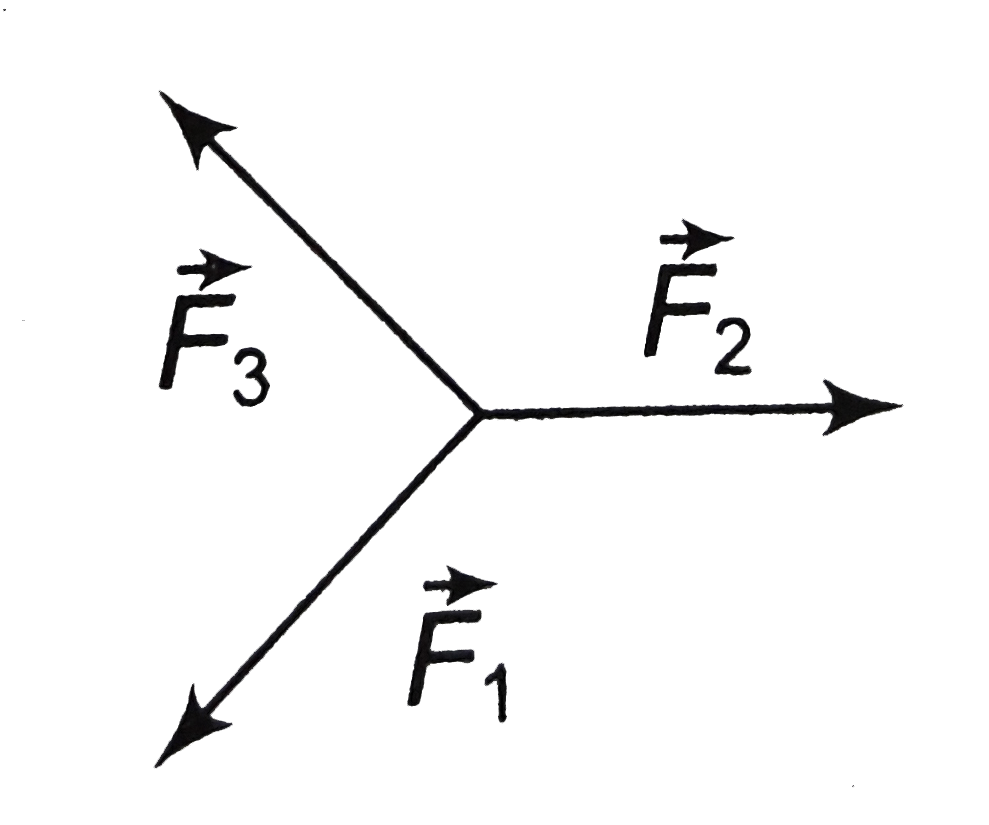
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Resultant Of Vectors24videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Expressing Vectors In Unit Vector Notation22videos
VECTORS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test28videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
How many minimum number of vectors in different planes can be added to give zero resultant ?
A2B3C4D5 - Question 2 - Select One
The minimum number of vector having different planes which can be added to give zero resultant is
A2B3C4D5 - Question 3 - Select One
The minimum number of Non -zero vector is :
A3B2C4D1
How many minimum numbers of a coplanar vector having different magntidues can be added to give zero resultant
View SolutionAssertion: Minimum number of non-equal Vectors in a plane required to give zero resultant is three.
Reason: If →A+→B+→C=→0, then they must lie in one planeView SolutionThe minimum number of unequal vectors whose vector sum can be zero is
View SolutionAssertion: The minimum number of non-coplanar Vectors whose sum can be zero, is four
Reason: The resultant of two vectors of unequal magnitude can be zero.View SolutionThe minimum number of vectors of equal magnitude required to produce a zero resultant is :
View Solution

