Question

Hydrogen atom in its ground state, is excited by means of monochromatic radiation of wavelength 975 Å . How many different lines are possible in the resulting spectrum ? Calculate the longest wavelength amongst them. Given, ionisation energy of hydrogen atom is 13.6 eV.

Explanation

Wavelength of incident radiation,
`lambda=975 "Å"=975 xx 10^(-8)` cm
`therefore` Energy of this photon,
`hf =(hc)/(lambda)`
=`(6.625xx10^(-27)xx3xx10^(10))/(975xx10^(-8)) erg`
`=(6.625xx10^(-27)xx3xx10^(10))/(975xx10^(-8)xx1.6xx10^(-12)eV =12.74 eV`
Ionisation energy of hydrogen atom =13.6 ev., the ground state energy of this atom =-13.6 eV . so, the energy of the excited state in which the atom is raised under the influence of incident radiation =-13.6+12.74=-0.86 eV.
The quantum number in the ground state = 1. so, if the quantum number in the excited state be n then
`-0.86 =-(13.6)/(n^2) or, n^2 =(13.6)/(0.86)=16 `(approx.)
so, n =4, i.e the excited state is the fourth Bohr orbit.
During transition from the fourth Bohr orbit to the ground state , the decrease in energy of the atom may occur in 6 different ways
[Fig.1.11] . As a result ,6 lines will be obtained in the spectrum.

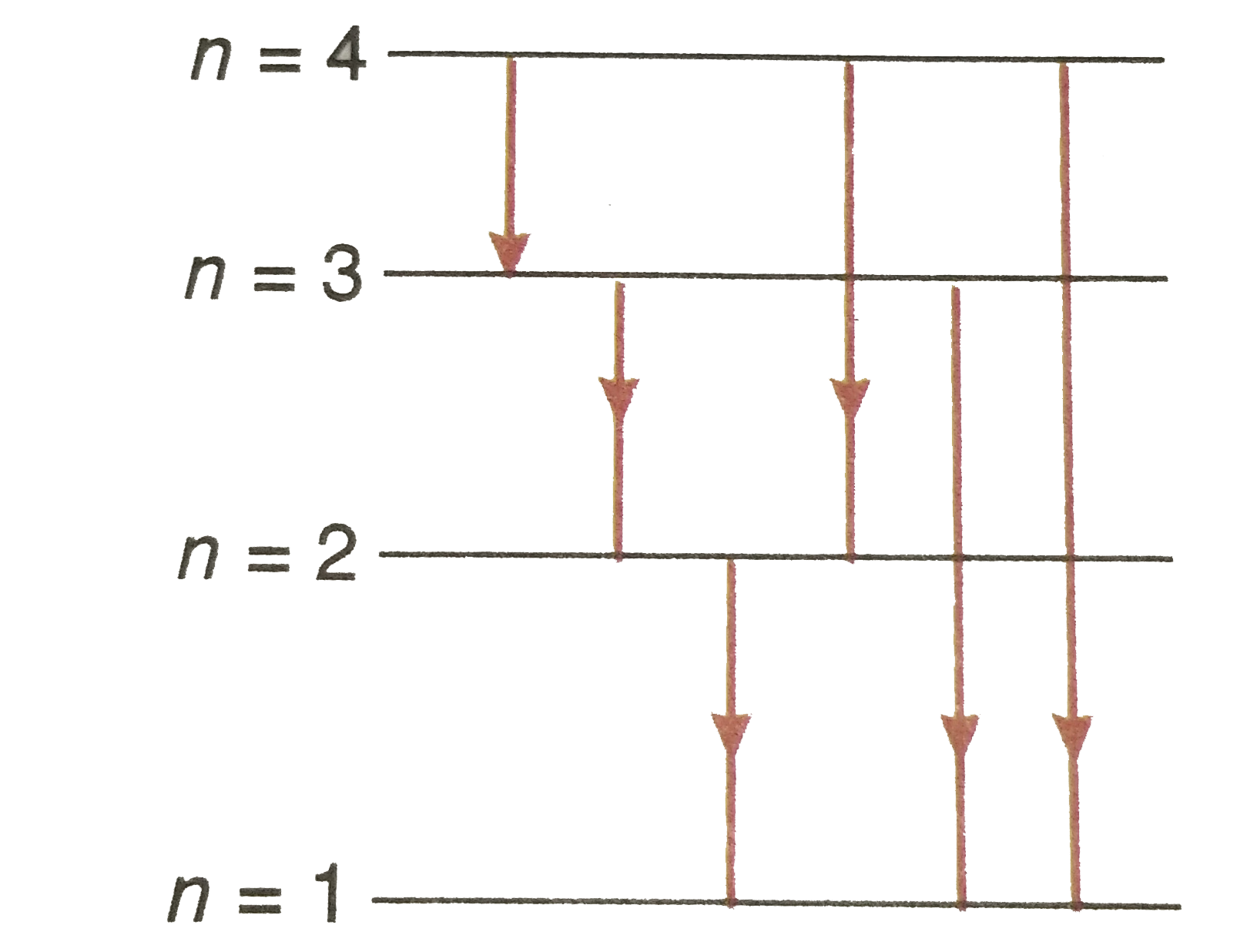
Of them, during transition from n=4 to n=3 , the energy difference is the least and hence in this case, the wavelength of the emitted spectral line will be maximum.
Energy of the third Bohr orbit =-`(13.6)/(3^2)=-1.51 eV`
`therefore` Decrease in energy due to transition form n =4 to n=3 =-0.86 -(-1.51)=0.65 eV.
Hence, the relation hf `=(hc)/(lambda)=E_4-E_3 ` gives,
`lambda=(hc)/(E_4-E_3)=(6.625xx10^(-27)xx3xx10^(10))/(0.65xx1.6xx10^(-12)) =19110xx10^(-8)cm =19110 "Å"`