(i) A cylindrical container has area of cross section equal to 4A and it contains a non viscous liquid of density 2ρ. A wooden cylinder of cross sectional area A and length L has density ρ. It is held vertically with its lower surface touching the liquid. It is released from this position. Assume that the depth of the container is sufficient and the cylinder does not touch the bottom.
(a) Find amplitude of oscillation of the wooden cylinder.
(b) Find time period of its oscillation.
Two cubical blocks of side length a and 2a are stuck symmetrically as shown in the figure. The combined block is floating in water with the bigger block just submerged completely. The block is pushed down a little and released. Find the time period of its oscillation. Neglect viscostiy.

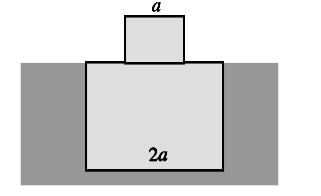
The correct Answer is:(i) (a) 3L8 (b)2π√3L8g
(ii) 3π√2ag
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
Two particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

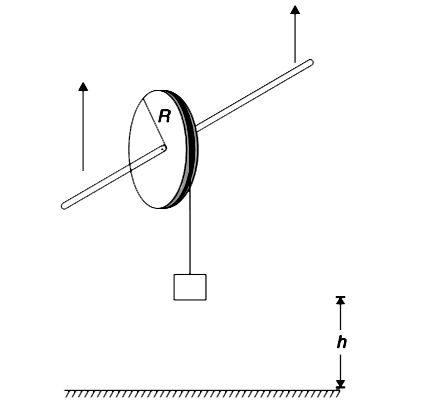
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
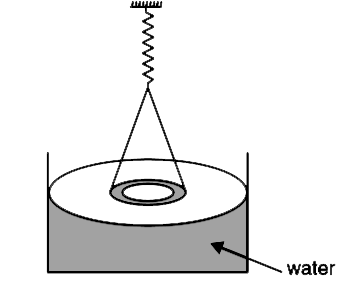
View SolutionA circular ring has inner and outer radii equal to 10mmand30mm respectively Mass of the ring is m=0.7 g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched 3.4cm from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is k=0.7Nm–1 find the surface tension of water.
View SolutionA cylindrical vessel contains a liquid of density rho up to height h . The liquid is closed by a piston of mass m and area of cross section A . There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
View SolutionTwo liquid columns of same height 5m and densities rho and 2rho are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
View SolutionA large tank of cross-section area A contains liquid of density ρ .A cylinder of density ρ4 ,length l=40cm ,and cross-section area a (<
View SolutionTwo non-mixing liquids of densities ρ and nρ(n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL(p<1) in the denser liquid. The density d is equal to
View SolutionTwo non -mixing liquids of densities ρ and np (n>1) are put in container . The height of each liquid is h.A solid cylinder of length L and density d is put in this container . The cylinder floats with its axis vertical and length PL(P<1) in the denser liquid .The density d is equal to .......
View SolutionTwo liquid columns of same height 5m and densities rho and 2rho are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
View SolutionTwo non-mixing liquids of densities ρ and n ρ(n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length PL (P<1) in the denser liquid. The density dis equal to
View SolutionA cylindrical vessel contains a liquid of density rho upto a heighth The liquid is closed by a piston of mass m and area of cross-section A. There is a small hole at the bottom of the vessel. Find the speed with which the liquid comes out of the hole
View SolutionTwo non-mixing liquids of densities ρ and n ρ(n>1) are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length PL (P<1) in the denser liquid. The density dis equal to
View Solution
