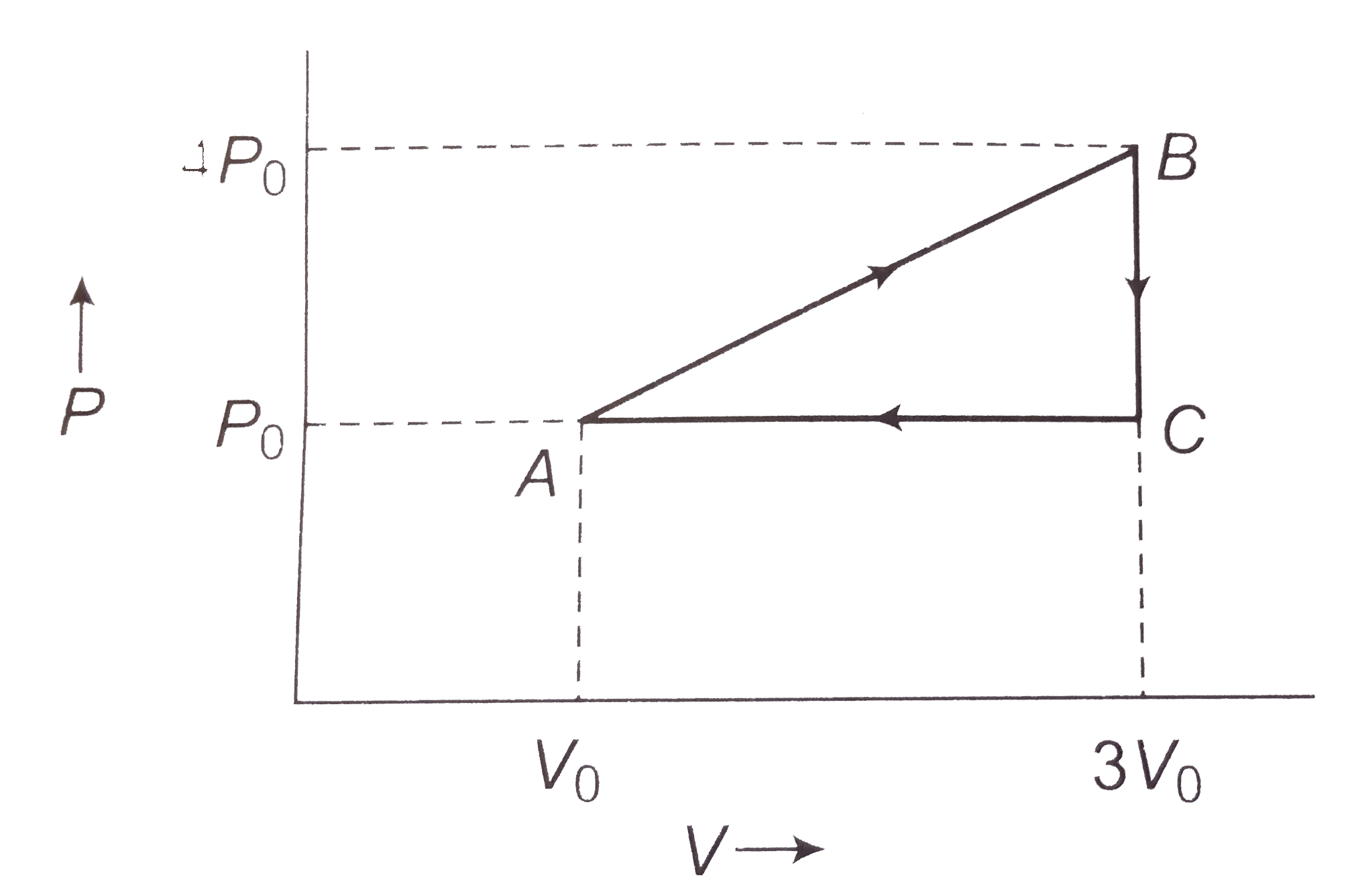
(i) ΔWAB=5P0V0
(ii) ΔWBC=0
(iii) ΔWCA=−2P0V0
(iv) ΔWABCA=3P0V0
(i),(iii)
(ii),(iii)
(iii),(iv)
all
The correct Answer is:D
ΔWAB=12(P0+4P0)(3V0−V0)=5P0V0
ΔWBC=0
ΔWCA=−P0(3V0−V0)=−2P0V0
ΔWABCA=ΔWAB+ΔW(BC)+ΔWCA=3P0V0
Topper's Solved these Questions
Similar Questions
Knowledge Check
ΔU+ΔW=0is valid for
AAdiabatic processBIsothermal processCIsobaric processDIsochoric process
A and B are two events such that P(A)=0.54,P(B)=0.69 and P(A∩B)=0.535.
(i) P(A∪B) (ii) P(A'∩B')
(iii) P(A∩B') (iv) P(B∩A')
View SolutionA and B are two events such that
P(A)=0.54,P(B)=0.69 and P(A∩B)=0.35
Find (i) P(A∪B) (ii) P(A'∩B')
(iii) P(A∩B') (iv)P(B∩A')
View Solution(a) Given two independent events A, B such that P(A)=0.3,P(B)=0.6. Find :
(i) P (A and B)
(ii) P (A and not B)
(iii) P (A or B)
(iv) P (neither A nor B).
(b) If P(A)=0.2,P(A∪B)=0.6, find P (B).
View SolutionSolve the following quadratic equations by factorisation method :
(i) x3−4x+3=0 (ii) m2−m−2=0 (iii)p2+9p+20=0
(iv)q2+q−12=0 (v) y2+2y−35=0 (vi)3x2+5x=0
(vii) x2−7x+12=0 (viii) x2−7x−18=0
View SolutionA and B are two events such that P(A)=0.54,P(B)=0.69 and P(A∩B)=0.36, then evaluate:
(i) P(A∪B) (ii) P(A'∩B')
(iii) (A∩B') (iv) P(B∩A')
View SolutionIf A and B are mutually exclusive events, P(A)=0.35 and P(B)=0.45, then find
(i) P(A')
(ii) P(B')
(iii) P(A∪B)
(iv) P(A∩B)
(v) P(A∩B')
(vi) P(A'∪B')
View SolutionA,B,C are events such that
Pr(A)=0.3,Pr(B)=0.4,Pr(C)=0.8
Pr(AB)=0.08,Pr(AC)=0.28 and Pr(B)=0.4,Pr(C)=0.8
If Pr(A∪B∪C)≥0.75, then show that Pr(BC) lies in the interval [0.23,0.48].
View Solution
