If a height h2 of water level is further decreases then:
cylinder will not move up and remains at original positoin.
for h2=H3, cylinder again starts moving up
for h2=H4, cylinder again starts moving up
for h2=H5, cylinder again starts moving up
The correct Answer is:A
When level of liquid is lowered below 4H/9 then liquid pressure is not able to lift the block and the block remains at its position.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (Assertion Reason Type Questions)
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (Matching Type Questions )
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (C. MCQ With More Than One Correct Answers)
12 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If height h2 of water level is further decreased, then
View SolutionWater is dripping out from a conical funnel of semi-vertical angle π4 at the uniform rate of 2cm2/sec in the surface through a tiny hole at the vertex of the bottom. When the slant height of the water level is 4 cm, find the rate of decrease of the slant heights of the water.
View Solution
Knowledge Check
A wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If height h2 of water level is further decreased, thenAcylinder will not move up and remains at its original positionBfor h2=H/3 , cylinder again starts moving upCfor h2=H/4 , cylinder again starts moving upDfor h2=H/5 , cylinder again starts moving upA wooden cylindrical of diameter 4r, height h and density ρ/3 is kept on a hole of diameter 2r of a tank , filled with water of density ρ as shown in the figure . The height of the base of cylinder from the base of tank is H .
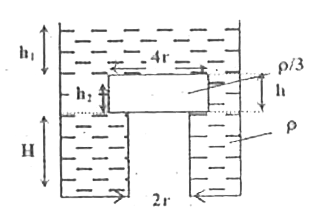
Let the cylinder is prevented from moving up , by applying a force and water level is further decreased . Then , height of water level (h2 in figure ) for which the cylinder remains in original position without application of force isAh/3B4h/9C2h/3DhA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external forceAh3B4h9C2h3Dh
Water is poured into a glass shaped as below at a change of the height the water level in the glass is change of the height of the water level in the glass is A. zero B. constant C. decreasing D. increasing
View SolutionWater pours out rate of Q from a tap, into a cylindrical vessel of radius r. The rate at which the height of water level rises the height is h, is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, then
View SolutionWater pours out rate of Q from a tap, into a cylindrical vessel of radius r. The rate at which the height of water level rises the height is h, is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, then
View Solution
