If a particle is moving on an parallel path given by r=bcosωtˆi+asinωtˆj, then find its radial acceleration along r
ωr
ω2r
−ω2r
none of these
(a) drdt=−bωtsinˆi+aωcosωtˆj
d2rdt2=−bω2sinωtˆi+aω2cosωtˆj
d2rdt2=−ω2[bcosωtˆi+asinωtˆj]=−ω2r
Topper's Solved these Questions
Similar Questions
A particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View SolutionA particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View Solution
Knowledge Check
A particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
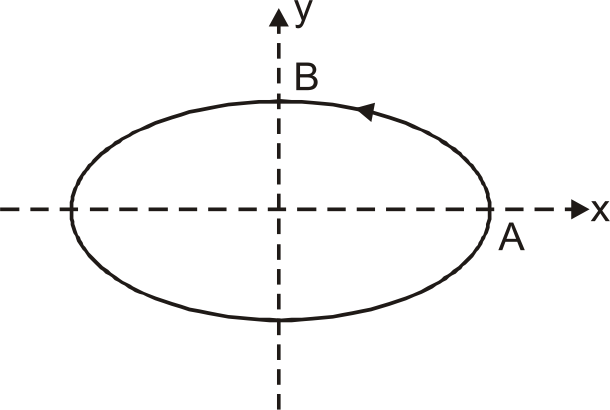 AContinuously increasesBcontinuously decreasesCRemains constantDfirst increases and then decreases
AContinuously increasesBcontinuously decreasesCRemains constantDfirst increases and then decreasesA particle is moving along an elliptical path with a constant speed. As it moves from A to B, magnitude of its acceleration:
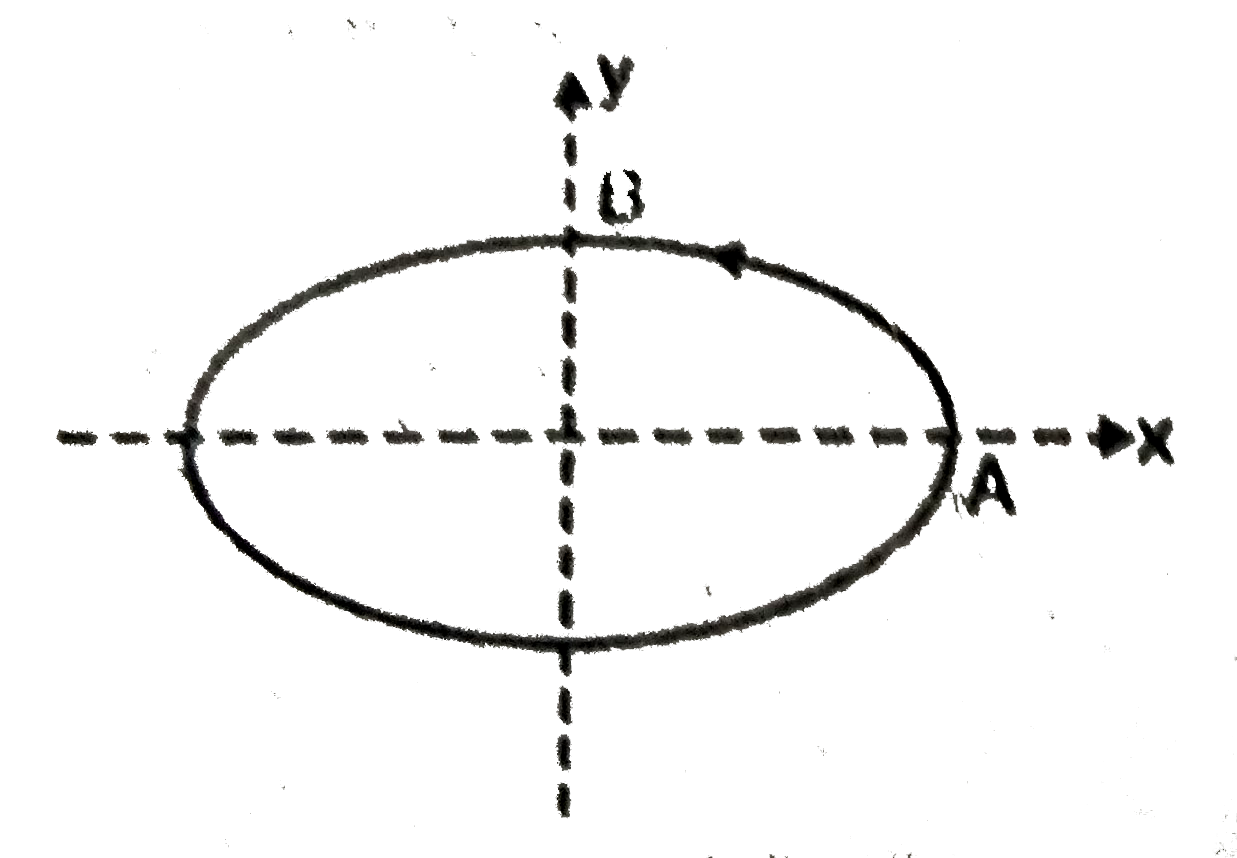 AContinuously increasesBcontinuoulsy decreasesCremains constantDfirst increases and then decreases
AContinuously increasesBcontinuoulsy decreasesCremains constantDfirst increases and then decreasesA particle of mass 0.2 kg moves along a path given by the relation : →r=2cosωtˆi+3sinωtˆj. Then he torque on the particle about the origin is :
A√13ˆkNmB√23ˆkNmC√32ˆkNmD0ˆk
A particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :

View SolutionA particle of mass 0.2 kg moves along a path given by the relation : →r=2cosωtˆi+3sinωtˆj. Then the torque on the particle about the origin is :
View SolutionConsider a particle moving in the x−y plane according to r=r(cosωtˆi+sinωtˆj), where r and ω are constants. Find the trajectory, the velocity, and the acceleration.

View SolutionFigure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
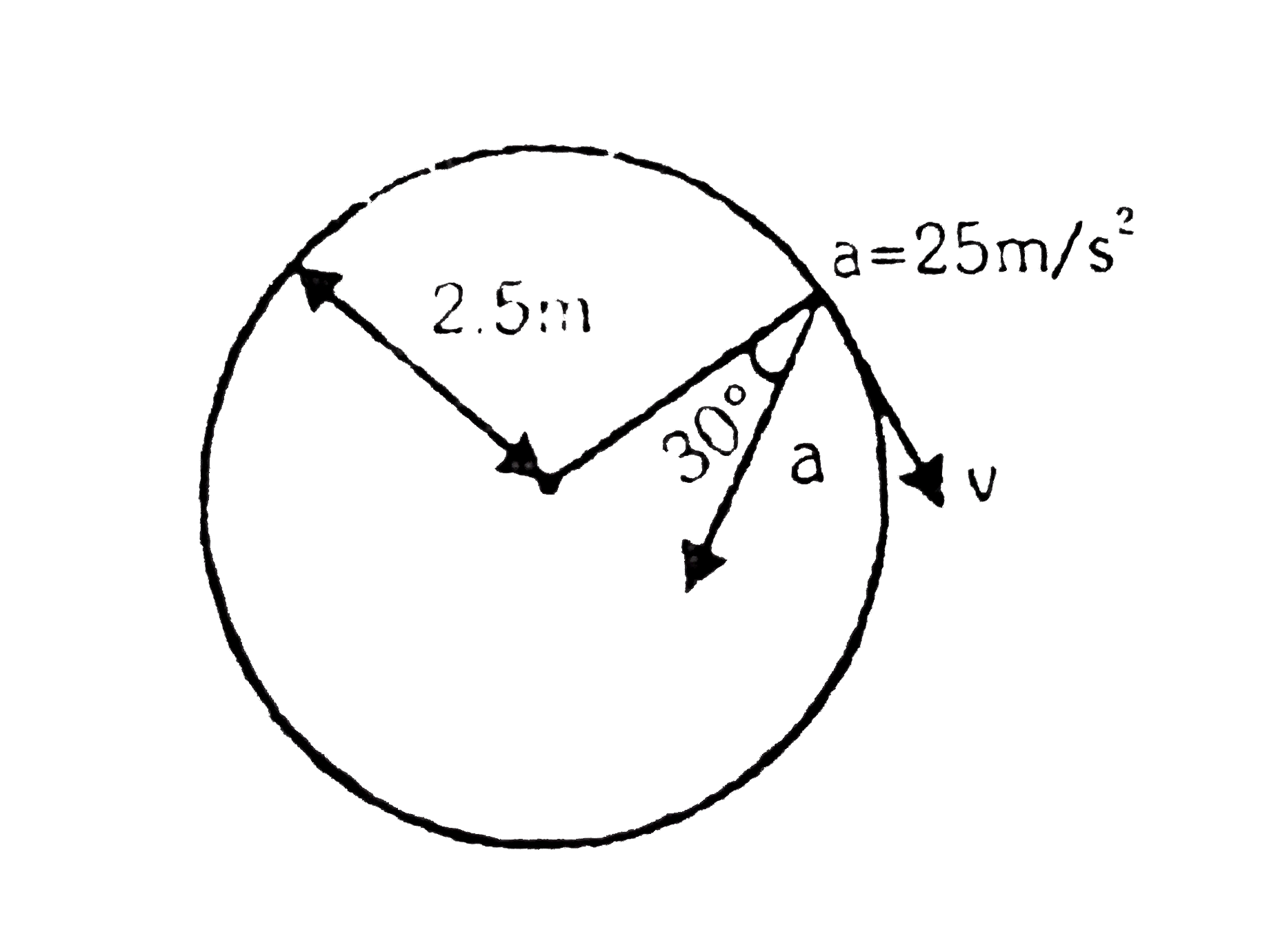
View SolutionIf s=a sinωtˆi+bcosωtˆj, the equation of path of particle is
View Solution
