If a particle moves from point P(2,3,5) to point Q(3,4,5). Its displacement vector be
ˆi+ˆj+10ˆk
ˆi+ˆj+5ˆk
ˆi+ˆj
2ˆi+4ˆj+6ˆk
The correct Answer is:C
To find the displacement vector of a particle moving from point P(2,3,5) to point Q(3,4,5), we can follow these steps:
Step 1: Identify the position vectors
The position vector of point P can be represented as:
→P=2^i+3^j+5^k
The position vector of point Q can be represented as:
→Q=3^i+4^j+5^k
Step 2: Write the formula for displacement vector
The displacement vector →D is given by the difference between the final position vector and the initial position vector:
→D=→Q−→P
Step 3: Substitute the position vectors into the formula
Substituting the position vectors we identified in Step 1:
→D=(3^i+4^j+5^k)−(2^i+3^j+5^k)
Step 4: Perform the vector subtraction
Now, we perform the subtraction component-wise:
→D=(3−2)^i+(4−3)^j+(5−5)^k
This simplifies to:
→D=1^i+1^j+0^k
Step 5: Write the final displacement vector
Thus, the displacement vector is:
→D=^i+^j
Summary
The displacement vector of the particle moving from point P(2,3,5) to point Q(3,4,5) is:
→D=^i+^j
The position vector of point P can be represented as:
→P=2^i+3^j+5^k
The position vector of point Q can be represented as:
→Q=3^i+4^j+5^k
The displacement vector →D is given by the difference between the final position vector and the initial position vector:
→D=→Q−→P
Substituting the position vectors we identified in Step 1:
→D=(3^i+4^j+5^k)−(2^i+3^j+5^k)
Now, we perform the subtraction component-wise:
→D=(3−2)^i+(4−3)^j+(5−5)^k
This simplifies to:
→D=1^i+1^j+0^k
Thus, the displacement vector is:
→D=^i+^j
The displacement vector of the particle moving from point P(2,3,5) to point Q(3,4,5) is:
→D=^i+^j
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Dot Product22videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Cross Product25videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Resultant Of Vectors24videos
VECTORS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test28videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If a particle moves from the point A(1,2,3) to the point B(4,6,9), its displacement vector be
Aˆi+ˆj+ˆkB2ˆi+3ˆj+4ˆkC3ˆi+4ˆj+6ˆkD3ˆi+4ˆj+5ˆk - Question 2 - Select One
Assertion (A) : The position of a particle on a rectangular coordinate system is (3,2,5). Then its position vector be 2ˆi+5ˆj+3ˆk.
Reason (R ) : The displacement vector of the particle that moves from point P(2,3,5) to point Q(3,4,5) is ˆi+ˆj.ABoth A and R are true and R is NOT the correct explanation of ABBoth A and R are true but R is NOT the correct explanation of ACA is true but R is falseDA is false but R is True - Question 3 - Select One
A force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
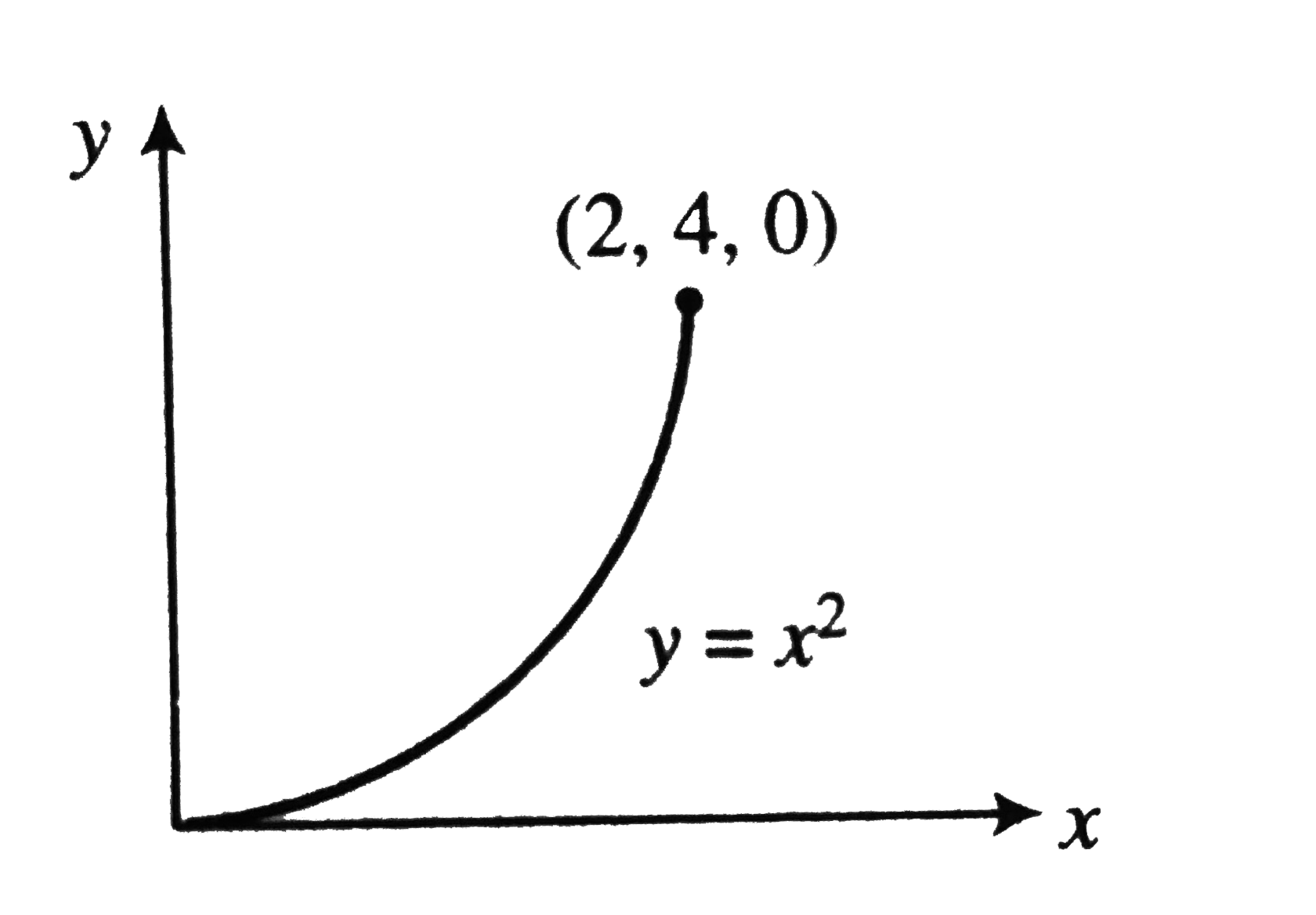 A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
The point of application of the force (-2,4,7) is displaced from the point (3,-5,1) to the point (5,9,7) .But the force is suddenly halved when the point of application moves half the
View SolutionTwo forces ˆi+ˆj+ˆkN and ˆi+2ˆj+3ˆkN act on a particle and displace it from (2,3,4) to point (5,4,3). Displacement is in m. work done is
View SolutionIn a two-dimensional motion of a particle, the particle moves from point A of position vector →r1, to point B of vectors are , respectively, r1=3andr2=4 and the angles they make with the x axis are θ1=75∘andθ2=15∘, respectively, then find the magnitude of the displacement vector.
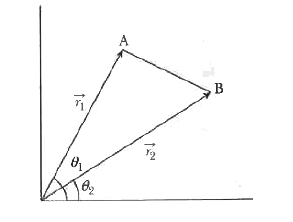 View Solution
View SolutionThe vector with initial point P(2,−3,5) and terminal point Q(3,−4,7) is :
View SolutionIf the constant due to which it is displaced from a point on a particle due to which it is displaced from a point A(4,−3,−2) to a point B(6,1,−3) then the work done by the forces is
View Solution

