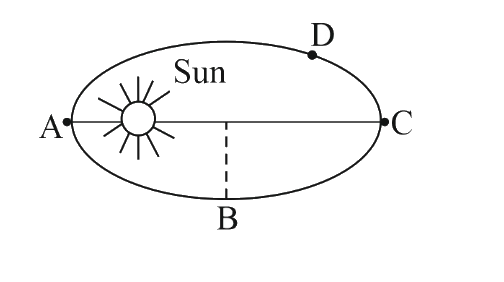
If a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is $r_{1}$ and maximum distance is $r_{2}$ . Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $[\frac{2 r_{1} r_{2}}{r_{1} + r_{2}}]$

Answer

Step by step video, text & image solution for If a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is r_(1) and maximum distance is r_(2). Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A planet is revolving around the sun as shown in elliptical path. The correct option is

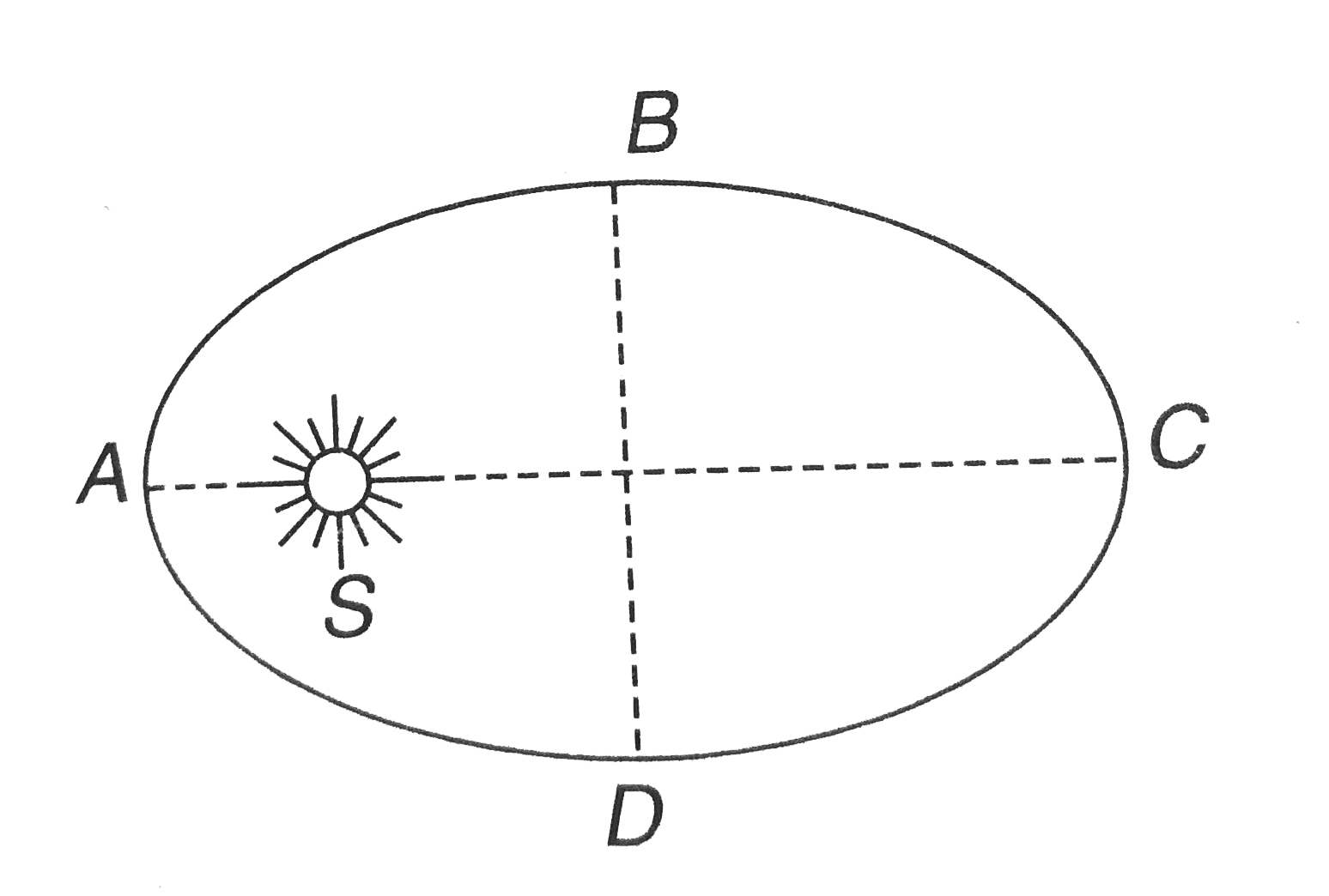AThe time taken in travelling DAB is less than that for BCD
BThe time taken in travelling DAB is greater than that for BCD
CThe time taken in travelling CDA is less than that for ABC
DThe time taken in travelling CDA is greater than that for ABC
Question 2 - Select One
A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with time
BThe total energ of the planet is constant and equals $- \frac{G m M_{s}}{2 a}, N_{s}$ is mass of sun
CTotal mechanical energy of the planet is constant and equals $- \frac{G m M_{s}}{a}, M_{2}$ is mass of sun
DDate is insufficient of arrice at a conclusion
Question 3 - Select One
The earth revolves around the sun in an elliptical orbit. It has a speed $v_{1}$ when it is at the minimum distance $d_{1}$ from the sun. When it is at the maximum distance $d_{2}$ from the sun, its speed is
A $\frac{v_{1} d_{2}}{d_{1}}$
B $\frac{v_{1} d_{1}}{d_{2}}$
C $v_{1}^{2} \frac{d_{2}}{d_{1}}$
D $v_{1} {(\frac{d_{1}}{d_{2}})}^{2}$

PHYSICS GALAXY - ASHISH ARORA-GRAVITATION-Particle Exercise

Home
Ask Doubt
Profile

If a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is r 1 and maximum distance is r 2 . Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse.

The correct Answer is: [ 2 r 1 r 2 r 1 + r 2 ]

Topper's Solved these Questions

Similar Questions

Knowledge Check

A planet is revolving around the sun as shown in elliptical path. The correct option is

A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :

The earth revolves around the sun in an elliptical orbit. It has a speed v1 when it is at the minimum distance d1 from the sun. When it is at the maximum distance d2 from the sun, its speed is

PHYSICS GALAXY - ASHISH ARORA-GRAVITATION-Particle Exercise

If a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is $r_{1}$ and maximum distance is $r_{2}$ . Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse.

The correct Answer is: $[\frac{2 r_{1} r_{2}}{r_{1} + r_{2}}]$

The earth revolves around the sun in an elliptical orbit. It has a speed $v_{1}$ when it is at the minimum distance $d_{1}$ from the sun. When it is at the maximum distance $d_{2}$ from the sun, its speed is