If a point moves along a circle with constant speed, prove that its angular speed about any point on the circle is half of that about the centre.
To prove that the angular speed of a point moving along a circle about any point on the circle is half of that about the center, we can follow these steps:
Step 1: Define the Circle and Points
Consider a circle with center C and radius R. Let M be a point on the circumference of the circle where a particle is moving with constant speed. Let O be another point on the circumference, which is directly opposite to M across the center C.
Step 2: Define Angular Displacement
Let the particle moving along the circle subtend an angle θ at the center C. The angular displacement θ corresponds to the arc length s traveled by the particle, where s=Rθ.
Step 3: Angular Speed about the Center
The angular speed ωC of the particle about the center C is defined as:
ωC=dθdt
This represents the rate of change of angular displacement with respect to time.
Step 4: Angular Displacement about Point M
Now, consider the angular displacement about point M. When the particle moves from point M to another point on the circle, it subtends an angle 2θ at point O (the opposite point on the circle). This is because the angle subtended at point O is twice that subtended at the center C.
Step 5: Angular Speed about Point O
The angular speed ωO about point O is given by:
ωO=d(2θ)dt=2dθdt=2ωC
Step 6: Relate Angular Speeds
From the above steps, we have:
ωO=2ωC
Thus, the angular speed about any point on the circumference (like O) is twice that about the center C.
Conclusion
Therefore, we can conclude that the angular speed about any point on the circle is half of that about the center:
ωO=12ωC
Consider a circle with center C and radius R. Let M be a point on the circumference of the circle where a particle is moving with constant speed. Let O be another point on the circumference, which is directly opposite to M across the center C.
Let the particle moving along the circle subtend an angle θ at the center C. The angular displacement θ corresponds to the arc length s traveled by the particle, where s=Rθ.
The angular speed ωC of the particle about the center C is defined as:
ωC=dθdt
This represents the rate of change of angular displacement with respect to time.
Now, consider the angular displacement about point M. When the particle moves from point M to another point on the circle, it subtends an angle 2θ at point O (the opposite point on the circle). This is because the angle subtended at point O is twice that subtended at the center C.
The angular speed ωO about point O is given by:
ωO=d(2θ)dt=2dθdt=2ωC
From the above steps, we have:
ωO=2ωC
Thus, the angular speed about any point on the circumference (like O) is twice that about the center C.
Therefore, we can conclude that the angular speed about any point on the circle is half of that about the center:
ωO=12ωC
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.1
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.2
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples
2 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Assertion : A body is moving along a circle with a constant speed. Its angular momentum about the centre of the circle remains constant
Reason : In this situation, a constant non-zero torque acts on the body.
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionA particle of mass 50 gm moving in a circle at 5 cm radius with a constant speed of 10 cm/s. What is its angular momentum about (i) centre of the circle, (ii) a point on the axis of the circle at 4 cm distance from its centre ? Which of these will be always in the same direction ? [Fig.]

View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View SolutionA point moves along a circle with speed v=at. The total acceleration of the point at a time when it has traced 1//8th of the circumference is:
View SolutionConsider a particle , moving in a circle with constant speed . P is a point outside the circle , in the same plane . Then , the angular momentum of the particle about the point P is
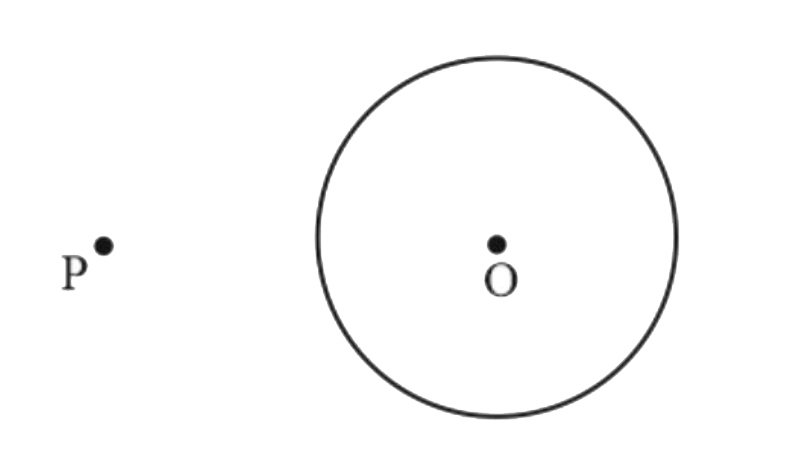
View SolutionWhen a body moves with a constant speed along a circle
View SolutionA horse runs along a circle with a speed of 20km/h . A lantern is at the centre of the circle. A fence is along the tangent to the circle at the point at which the horse starts. Find the speed with which the shadow of the horse moves along the fence at the moment when it covers 1/8 of the circle in km/h.
View SolutionA particle moves in a circular path with constant speed .Find out a point about which the angular momentum of the particle is constant and another point about which changes with time.
View SolutionA point charge is moving in clockwise direction in a circle with constant speed. Consider the magnetic field produced by the charge at a fiexed point P (not at the centre of circle ) on the axis of the circle. Then,
View Solution
