If both the length of an antenna and the wavelength of the signal to be transmitted are doubled, the power radiated by the antenna
is doubled
is halved
remains constant
is quadrupled
The correct Answer is:C
To solve the problem, we need to analyze how the power radiated by an antenna changes when both the length of the antenna (L) and the wavelength of the signal (λ) are doubled.
1. Understand the relationship between power, length, and wavelength:
The power radiated by an antenna is given by the formula:
P∝Lλ2
where P is the power radiated, L is the length of the antenna, and λ is the wavelength of the signal.
2. Define the initial conditions:
Let the initial length of the antenna be L and the initial wavelength be λ. Thus, the initial power can be expressed as:
P=kLλ2
where k is a proportionality constant.
3. Apply the changes to the length and wavelength:
According to the problem, both the length of the antenna and the wavelength are doubled:
- New length L′=2L
- New wavelength λ′=2λ
4. Calculate the new power:
Substitute the new values into the power formula:
P′=kL′λ′2=k2L(2λ)2
5. Simplify the expression:
Now simplify the equation:
P′=k2L4λ2=kL2λ2
6. Compare the new power with the initial power:
Notice that:
P′=12(kLλ2)=12P
This indicates that the new power P′ is half of the initial power P.
Conclusion:
The power radiated by the antenna is halved when both the length of the antenna and the wavelength of the signal are doubled.
Final Answer:
The power radiated by the antenna will be half of the original power.
---
The power radiated by an antenna is given by the formula:
P∝Lλ2
where P is the power radiated, L is the length of the antenna, and λ is the wavelength of the signal.
Let the initial length of the antenna be L and the initial wavelength be λ. Thus, the initial power can be expressed as:
P=kLλ2
where k is a proportionality constant.
According to the problem, both the length of the antenna and the wavelength are doubled:
- New length L′=2L
- New wavelength λ′=2λ
Substitute the new values into the power formula:
P′=kL′λ′2=k2L(2λ)2
Now simplify the equation:
P′=k2L4λ2=kL2λ2
Notice that:
P′=12(kLλ2)=12P
This indicates that the new power P′ is half of the initial power P.
The power radiated by the antenna is halved when both the length of the antenna and the wavelength of the signal are doubled.
The power radiated by the antenna will be half of the original power.
Topper's Solved these Questions
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS
20 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - NCERT
9 Videos
- ATOMS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ATOMS EXERCISE - Assertion And Reason
15 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
I=P4πr2
At a large distance r from a radio antenna, the intensity of the radio signal I is related to the power of the signal P by the formula above.
Which of the following expresses the square of the distance from the radio antenna in terms of the intensity of the radio signal and the power of the signal?Ar2=IP4πBr2=P4πICr2=4πIPDr2=I4πPI=P4πr2
At a large distance r from a radio antenna, the intensity of the radio signal I is related to the power of the signal P by the formula above.
For the same signal emitted by a radio antenna, Observer A measures its intensity to be 16 times the intensity measured by Observer B. The distance of Observer A from the radio antenna is what fraction of the distance of Observer B from the radio antenna?A14B116C164D1256
The power of a motor is 200W. If the unit of length is halved, that of mass is doubled and that of time is aiso doubled, then the power of the motor in the new system is
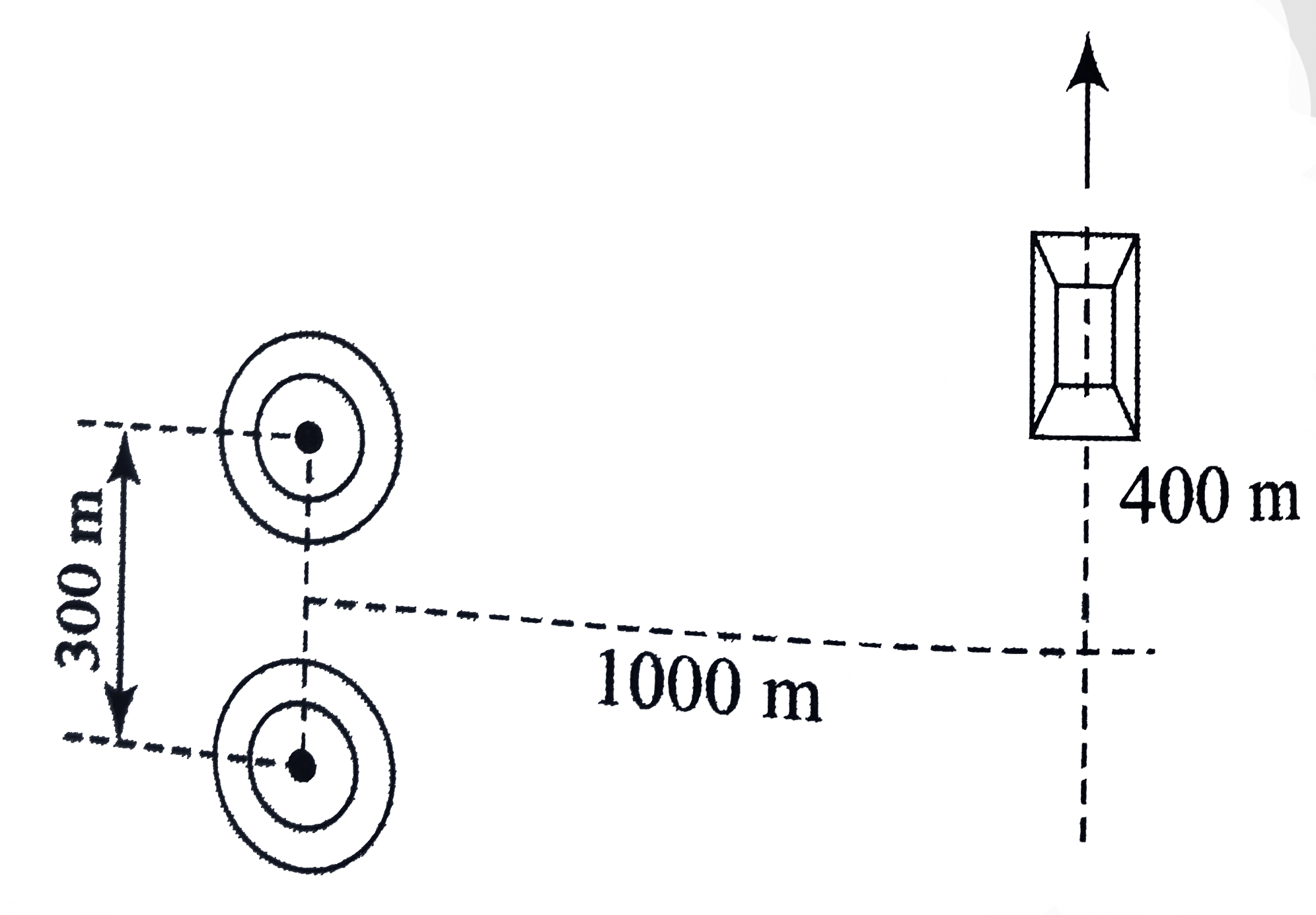
View SolutionTwo radio antennas separated by 300 m as shown in figure simultaneously broadcast indentical singals at the same wavelength. A radio in a car traveling due north receives the signals. (a) If the car is at the position of the second maximum, what is the wavelength of the signals? (b) How much farther must the car travel to encounter the next mininum in reception? (Note: Do not use the small- angle approximation in this problem.)
View SolutionThe length of half wave dipole antenna at 50 MHz is
View SolutionHow does the effective power radiated by an antenna vary with wavelength?
View Solution(A) : For transmitting a signal, the antenna should have a size comparable to wave length of the signal at least λ/4 in dimension
(R) : The antenna properly senses the time variation of the signal
View SolutionThe length of the antenna
a) limits the frequency of EM waves to be radiated
b) makes the users to opt for Higher frequency transmission
c) is insignificant during transmission.
View Solution
