If identical charges (−q) are placed at each corner of a cube of side b, then electric potential energy of charge (+q) which is palced at centre of the cube will be
8√2q24πε0b
−8√2q2πε0b
−4√2q2πε0b
−4q2√3πε0b
The correct Answer is:D
To find the electric potential energy of a charge +q placed at the center of a cube with identical charges −q at each corner, we can follow these steps:
Step 1: Understand the Setup
We have a cube with side length b and a charge +q placed at the center of the cube. Each corner of the cube has a charge −q.
Step 2: Calculate the Distance from the Center to a Corner
The distance from the center of the cube to any corner can be calculated using the diagonal of the cube. The formula for the length of the diagonal d of a cube with side length b is given by:
d=b√3
Since we need the distance from the center to a corner, we take half of this diagonal:
L=d2=b√32
Step 3: Calculate the Electric Potential Energy
The electric potential energy U of the charge +q due to one charge −q is given by the formula:
U=kq1q2r
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between them.
Since there are 8 identical charges −q at the corners, the total potential energy U due to all these charges is:
U=8∑i=1k(+q)(−q)L
This simplifies to:
U=8(k(+q)(−q)L)=−8kq2L
Step 4: Substitute the Value of L
Now substitute L=b√32 into the equation:
U=−8kq2b√32=−8k2q2b√3=−16kq2b√3
Step 5: Substitute the Value of k
Coulomb's constant k can be expressed as:
k=14πϵ0
Substituting this into the equation gives:
U=−16⋅14πϵ0⋅q2b√3=−4q2πϵ0b√3
Final Answer
Thus, the electric potential energy of the charge +q placed at the center of the cube is:
U=−4q2πϵ0b√3
We have a cube with side length b and a charge +q placed at the center of the cube. Each corner of the cube has a charge −q.
The distance from the center of the cube to any corner can be calculated using the diagonal of the cube. The formula for the length of the diagonal d of a cube with side length b is given by:
d=b√3
Since we need the distance from the center to a corner, we take half of this diagonal:
L=d2=b√32
The electric potential energy U of the charge +q due to one charge −q is given by the formula:
U=kq1q2r
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between them.
U=8∑i=1k(+q)(−q)L
This simplifies to:
U=8(k(+q)(−q)L)=−8kq2L
Now substitute L=b√32 into the equation:
U=−8kq2b√32=−8k2q2b√3=−16kq2b√3
Coulomb's constant k can be expressed as:
k=14πϵ0
Substituting this into the equation gives:
U=−16⋅14πϵ0⋅q2b√3=−4q2πϵ0b√3
Thus, the electric potential energy of the charge +q placed at the center of the cube is:
U=−4q2πϵ0b√3
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Euipotentials
45 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor
32 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Relation Between Electric Field And Potential
24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
If 8 identical charges of -g each are placed at the eight corners of a cube of side b, then electrostatic potential energy of a charge +q0 placed at the centre of the cube will be
A8√2qq04πε0bB−8√2qq04πε0bC+4qq0√3πε0bD−4qq0√3πε0bA charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
A8Qπε0aB4Q4πε0aC4Q√3πε0aD2Qπε0aA charge +q is placed at the mid point of a cube of side L. The electric flux emerging from cube is
Aq∈0Bq6L2∈0C6qL2∈0Dzero
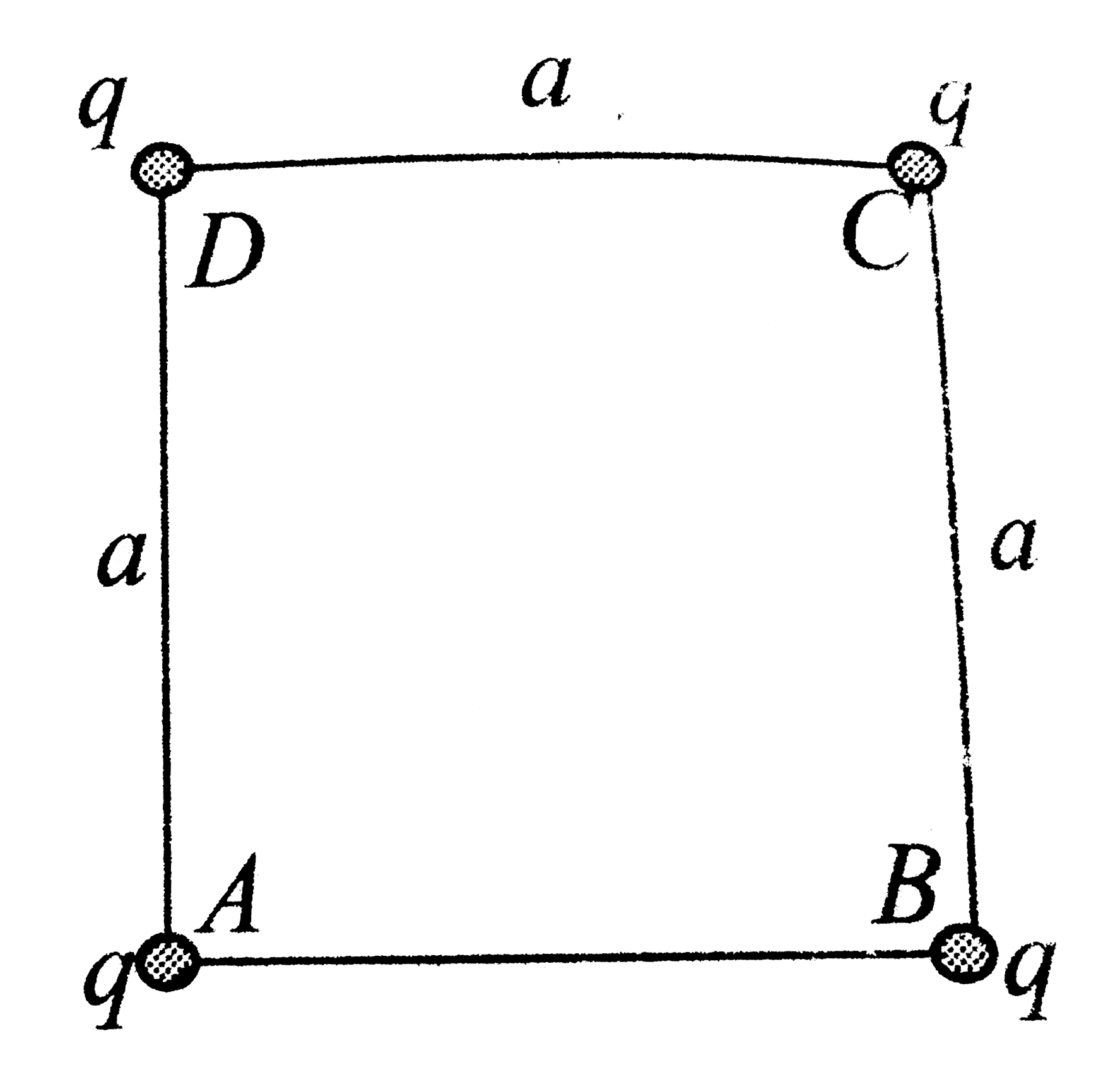
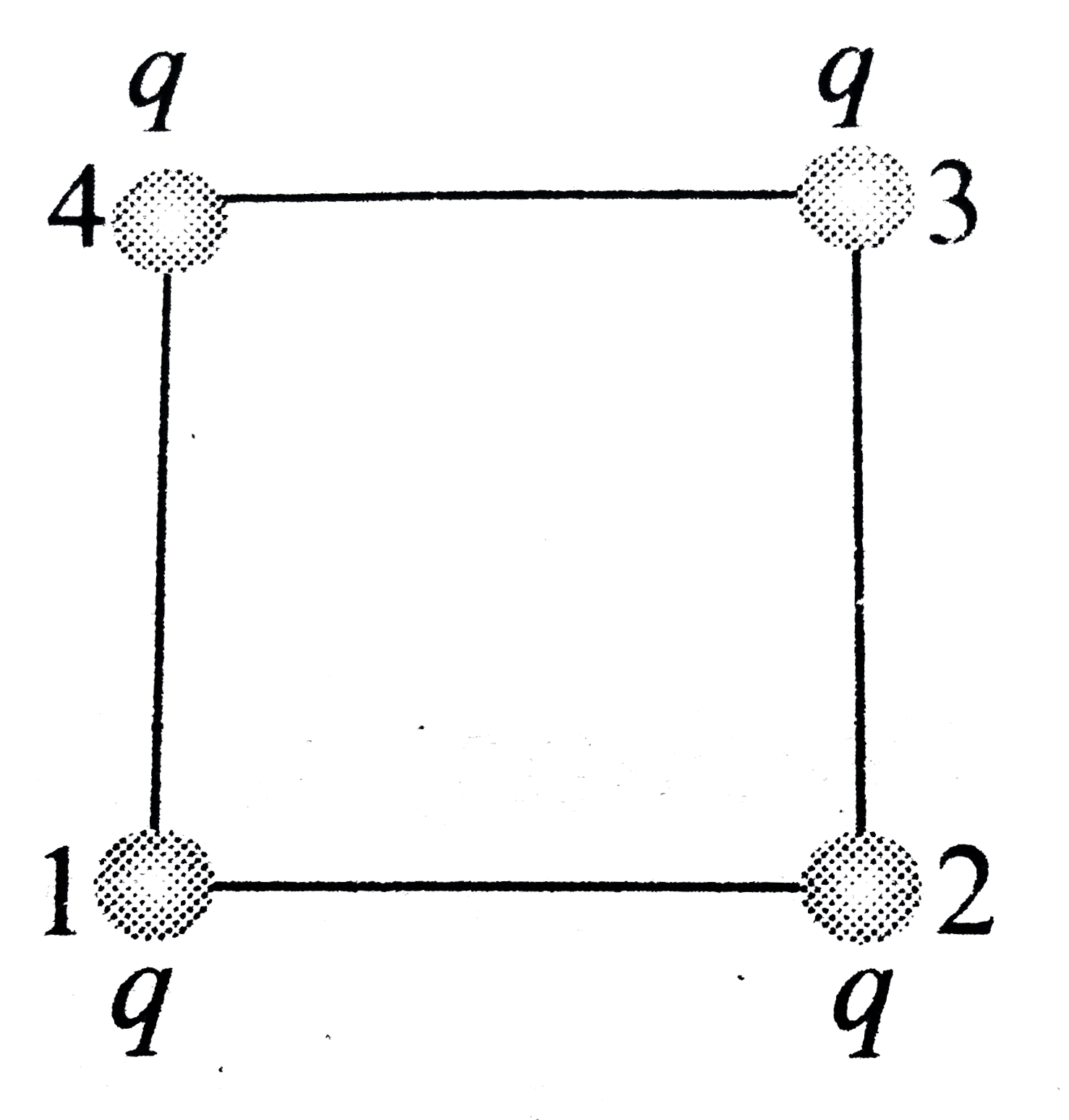
Four identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionAn electric charge q is placed at the centre of a cube of side l. The electric flux through one of its faces will be
View SolutionAn electric charge q is placed at the centre of a cube of side l. The electric flux through one of its faces will be
View SolutionA point charge +q is placed at the mid point of a cube of side L. The electric flux emerging from the cube is :
View SolutionA point charge +q is placed at the mid point of a cube of side L. The electric flux emerging from the cube is :
View Solution

 .
.