If K.E of a body is made three times , how will the momentum change ?
To solve the problem of how momentum changes when the kinetic energy of a body is made three times, we can follow these steps:
Step 1: Understand the relationship between kinetic energy and momentum
The kinetic energy (K.E) of a body is given by the formula:
K.E=P22m
where P is the momentum and m is the mass of the body.
Step 2: Set up the initial and final kinetic energy
Let the initial kinetic energy be K.E1=k and the final kinetic energy be K.E2=3k.
Step 3: Write the equations for kinetic energy
From the kinetic energy formula, we can express the initial and final kinetic energies in terms of momentum:
K.E1=P2i2m
K.E2=P2f2m
where Pi is the initial momentum and Pf is the final momentum.
Step 4: Substitute the kinetic energy values
Substituting the values of kinetic energy into the equations, we have:
k=P2i2m
3k=P2f2m
Step 5: Eliminate mass from the equations
We can eliminate m by multiplying both equations by 2m:
2mk=P2i
6mk=P2f
Step 6: Relate the two equations
Now, we can relate the two equations:
P2f=3⋅P2i
Step 7: Find the final momentum
Taking the square root of both sides gives us:
Pf=√3⋅Pi
Conclusion
Thus, when the kinetic energy is made three times, the momentum changes according to the relation:
Pf=√3⋅Pi
The kinetic energy (K.E) of a body is given by the formula:
K.E=P22m
where P is the momentum and m is the mass of the body.
Let the initial kinetic energy be K.E1=k and the final kinetic energy be K.E2=3k.
From the kinetic energy formula, we can express the initial and final kinetic energies in terms of momentum:
K.E1=P2i2m
K.E2=P2f2m
where Pi is the initial momentum and Pf is the final momentum.
Substituting the values of kinetic energy into the equations, we have:
k=P2i2m
3k=P2f2m
We can eliminate m by multiplying both equations by 2m:
2mk=P2i
6mk=P2f
Now, we can relate the two equations:
P2f=3⋅P2i
Taking the square root of both sides gives us:
Pf=√3⋅Pi
Thus, when the kinetic energy is made three times, the momentum changes according to the relation:
Pf=√3⋅Pi
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Revision Exercise (Additional Questions)3videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Revision Exercise (Fill in the blanks)10videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Higher Order Thinking Skills & Advanced Level15videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
If the K.E. of a body is increased by 300%, its momentum will increase by
A100 %B15 %C√300%D17.5 % - Question 2 - Select One
If the KE of a body becomes four times its initial value, then the new momentum will be more than its initial momentum by,
A0.5B1C1.25D1.5 - Question 3 - Select One
If the KE of a body becomes four times its initial value, then the new momentum will be more than its initial momentum by,
A50%B100%C125%D150%
Can the K.E. of a body be negative
View SolutionIF the K.E of a body increases by 200 % then what will be the parcentage increases of momentum ?
View SolutionThe velocity of an aeroplane is made twice (a) What will happen to the momentum? Will the momentum remain conserved? (b) What will happen to the K.E.? Will the energy remain conserved ?
View SolutionA force-time graph for the motion of a body is shown in the figure. The change in the momentum of the body between zero and 10sec is
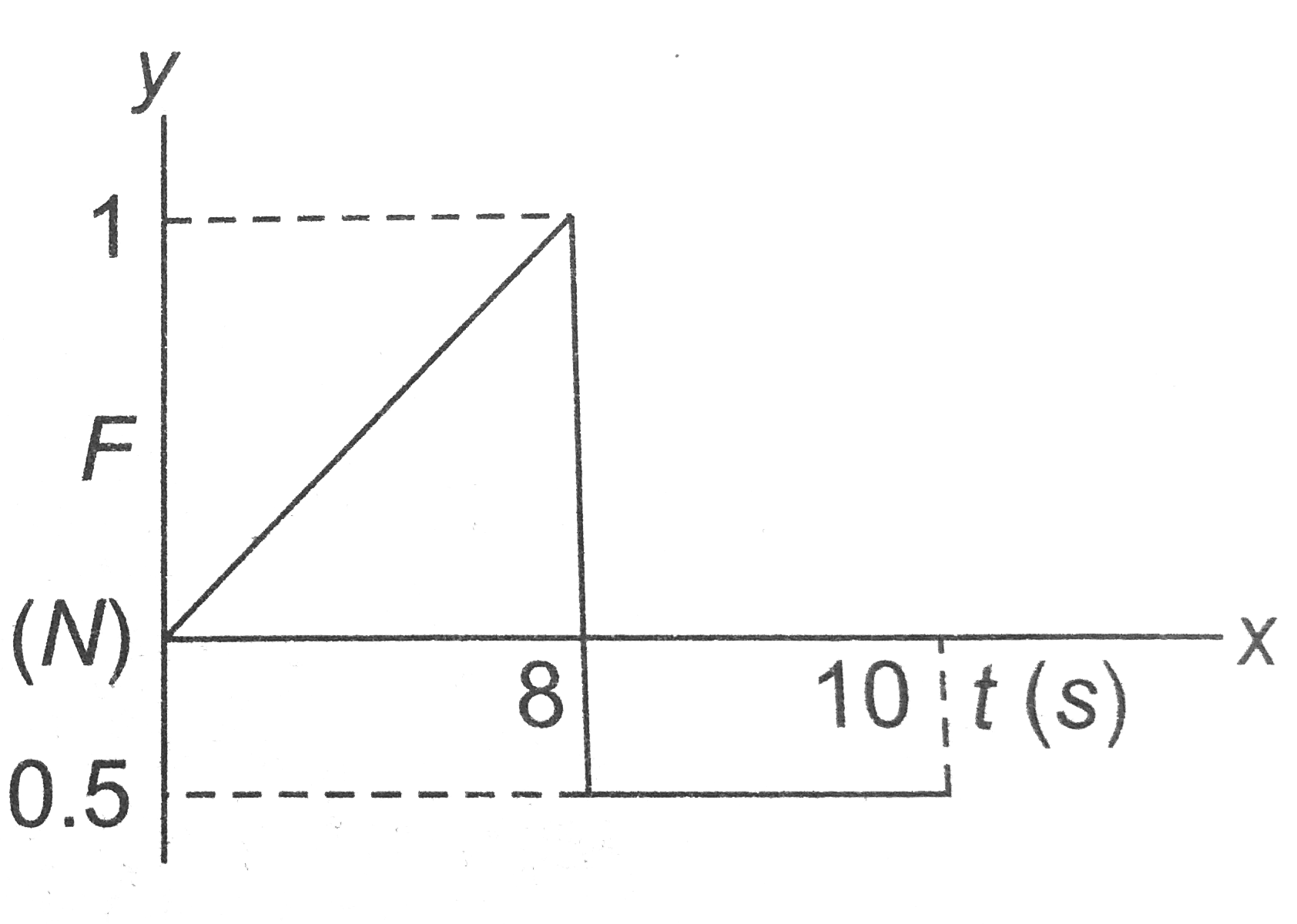 View Solution
View SolutionIf the K. E of a body is increased by 300% ,its momentum will increase by :
View Solution

