If μ1,μ2 are refractive indices of a body and its surrounding medium respectively, then the body would disappear if
μ1>μ2
μ1<μ2
μ1=μ2
μ1≥μ2
The correct Answer is:C
To determine when a body would disappear in a surrounding medium based on their refractive indices, we can analyze the conditions under which light behaves when passing from one medium to another.
1. Understanding Refractive Indices:
- Let μ1 be the refractive index of the body and μ2 be the refractive index of the surrounding medium.
- The refractive index is a measure of how much light slows down in a medium compared to its speed in a vacuum.
2. Condition for Disappearance:
- A body will disappear when light passes through it without bending or reflecting. This occurs when the refractive indices of the body and the surrounding medium are equal, i.e., μ1=μ2.
3. Behavior of Light:
- When μ1=μ2, light rays entering the body do not change speed or direction. They travel straight through the body and exit without any deviation.
- Since there is no bending or reflection of light at the interface, the body becomes invisible to an observer.
4. Other Conditions:
- If μ1>μ2: The body is denser than the surrounding medium. Light rays will bend towards the normal upon entering the body, making it visible.
- If μ1<μ2: The body is less dense than the surrounding medium. Light rays will bend away from the normal, also making it visible.
5. Conclusion:
- Therefore, the body will disappear only when μ1 is equal to μ2.
Final Answer:
The body would disappear if μ1=μ2.
---
- Let μ1 be the refractive index of the body and μ2 be the refractive index of the surrounding medium.
- The refractive index is a measure of how much light slows down in a medium compared to its speed in a vacuum.
- A body will disappear when light passes through it without bending or reflecting. This occurs when the refractive indices of the body and the surrounding medium are equal, i.e., μ1=μ2.
- When μ1=μ2, light rays entering the body do not change speed or direction. They travel straight through the body and exit without any deviation.
- Since there is no bending or reflection of light at the interface, the body becomes invisible to an observer.
- If μ1>μ2: The body is denser than the surrounding medium. Light rays will bend towards the normal upon entering the body, making it visible.
- If μ1<μ2: The body is less dense than the surrounding medium. Light rays will bend away from the normal, also making it visible.
- Therefore, the body will disappear only when μ1 is equal to μ2.
The body would disappear if μ1=μ2.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - MCGROW HILL PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING QUESTIONS
37 Videos
- REFLECTION OF LIGHT BOOK - MCGROW HILL PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - HIGHER ORDER THINKING QUESTIONS
10 Videos
- SOURCES OF ENERGY BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS
82 Videos
Similar Questions
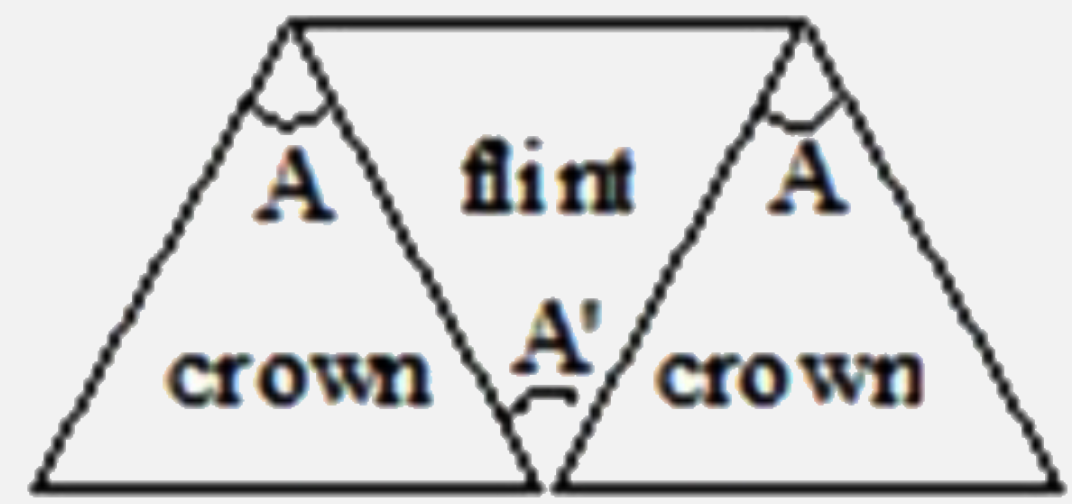
Three thin prisms are combined as shown in figure . The refractive indices of the crown glass for red , yellow and violet rays are μr,μyandμv respectively and those for the flint glass are μr',μy'andμv' respectively . Find the ratio A'A for which , there is no net angular dispersion (A and A' are respective deviations )
View SolutionIf μv,μr,μb are refractive indices of violet, red and blue, respectively, in a given medium, then
View Solution
Knowledge Check
If μ1andμ2are aboslute refractive index of medium 1 and medium 2 respectively, then
A1μ2=μ1μ2B1μ2=μ2μ1C1μ2=μ1μ2D1μ2=1μ1μ2If refractive index of core & cladding are μ1&μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of theseIf refractive index of core & cladding are μ1 & μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of these
If μ1andμ2 are the refractive indices of the material of core and cladding respectively of an optical fiber, then
View SolutionRefractive index (μ) of a medium depends upon
View SolutionIf μ1 and μ2 are the refractive indices of the materials of core and cladding of an optical fibre, then the loss of light due to its leakage can be minimized by having
View SolutionIn the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive indices
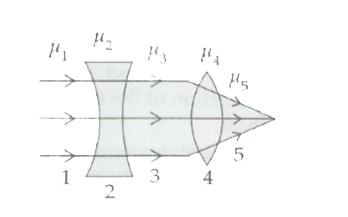
of the mediums 1,2,3,4 and 5 respectively . Consider the following
(1) μ1=μ2 (2) μ3=μ4=μ5
μ2<μ3 (4) μ4>μ5
View SolutionIf μ and μ2 are the refractive indices of the materials of core and cladding of an optical fibre, then loss of light due to its leakage can be minimised by having
View Solution
