If n is the rigidity modulus, r is the radius , l is the length and C is the moment of the couple, then has the dimensions of
Angle
Mass
Length
Frequency
The correct Answer is:A
To solve the problem, we need to find the dimensions of the expression (2lc)/(πnr4) where n is the rigidity modulus, r is the radius, l is the length, and C is the moment of the couple.
Step 1: Determine the dimensions of each variable
1. Rigidity Modulus (n):
- The rigidity modulus is defined as stress divided by strain.
- Stress = Force/Area = F/A = N/m2 = kg⋅m−1⋅s−2.
- Strain = Change in length/original length (dimensionless).
- Therefore, the dimensions of rigidity modulus n are:
(n)=(Stress)=(F/A)=(ML−1T−2)
2. Length (l):
- The dimension of length is:
(l)=(L)
3. Moment of Couple (C):
- The moment of a couple is defined as force multiplied by the distance (lever arm).
- Dimensions of force F = kg⋅m/s2 = MLT−2.
- Therefore, the dimensions of the moment of couple C are:
(C)=(F)⋅(Distance)=(MLT−2)⋅(L)=(ML2T−2)
4. Radius (r):
- The dimension of radius is:
(r)=(L)
Step 2: Substitute the dimensions into the expression
Now we substitute these dimensions into the expression (2lc)/(πnr4):
2lcπnr4
- The dimensions of 2lc are:
(l)⋅(C)=(L)⋅(ML2T−2)=(ML3T−2)
- The dimensions of n and r4 are:
(n)=(ML−1T−2),(r4)=(L4)
Step 3: Combine the dimensions
Now we can combine everything:
(ML3T−2)(ML−1T−2)⋅(L4)=(ML3T−2)(ML4−1)⋅(T−2)=(ML3T−2)(ML3T−2)=1
Step 4: Conclusion
The expression (2lc)/(πnr4) is dimensionless.
Final Answer
Thus, the dimensions of (2lc)/(πnr4) are dimensionless, which corresponds to the option of "angle" since angles are often considered dimensionless.
- The rigidity modulus is defined as stress divided by strain.
- Stress = Force/Area = F/A = N/m2 = kg⋅m−1⋅s−2.
- Strain = Change in length/original length (dimensionless).
- Therefore, the dimensions of rigidity modulus n are:
(n)=(Stress)=(F/A)=(ML−1T−2)
- The dimension of length is:
(l)=(L)
- The moment of a couple is defined as force multiplied by the distance (lever arm).
- Dimensions of force F = kg⋅m/s2 = MLT−2.
- Therefore, the dimensions of the moment of couple C are:
(C)=(F)⋅(Distance)=(MLT−2)⋅(L)=(ML2T−2)
- The dimension of radius is:
(r)=(L)
(l)⋅(C)=(L)⋅(ML2T−2)=(ML3T−2)
(n)=(ML−1T−2),(r4)=(L4)
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A STRAIGHT LINE
59 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Knowledge Check
The young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
AY2BYC2YD4Y
The young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced toL2 and radius r2 , then its young's modulus will be
View SolutionThe area of a regular polygon of n sides is (where r is inradius, R is circumradius, and a is side of the triangle) nR22sin(2πn) (b) nr2tan(πn) na24cotπn (d) nR2tan(πn)
View SolutionThe Young's modulus of a wire of length L and radius r is Y newton/m2. If the length of the wire is dooubled and the radius is reduced to r2, its Young's modulus will be
View SolutionA copper wire of length l and radius r is nickel plated till its final radius is 2r. If the resistivity of the copper and nickel are ρc and ρn, then find the equivalent resistance of the wire.
View SolutionThe area of a regular polygon of n sides is (where r is inradius, R is circumradius, and a is side of the triangle (a) nR22sin(2πn) (b) nr2tan(πn) (c) na24cotπn (d) nR2tan(πn)
View SolutionTwo wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a width mg, fig. What is the net elongation in the two wires?
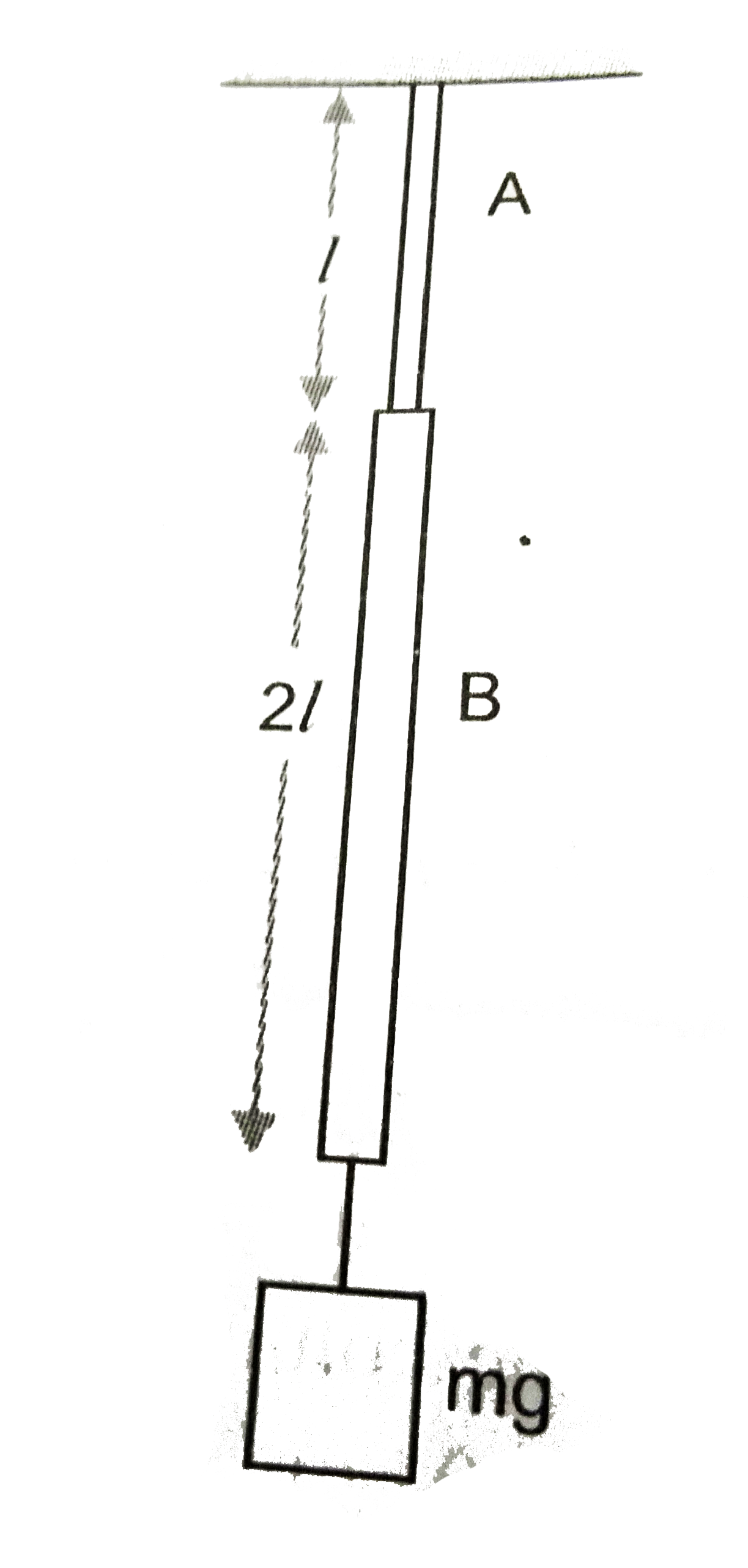
View Solution
