If the areas under the I−H hysteresis loop and BH hysteresis loop are denoted by A1 and A2, then
A2=μ0A1
A2=A1
A2=A1μ0
A2=μ20A1
The correct Answer is:A
As, B=μ0(H+l)
⇒ dB=μ0dH+μ0dl
or ∮HdB=μ0∮HdH+μ0∮Hdl
∮HdH=0
∮HdB=μ0∮H.dl
Area of the B-H loop =μ0× area of l - H loop
i.e. A2=μ0A1
Topper's Solved these Questions
- MAGNETOSTATICS BOOK - BITSAT GUIDECHAPTER - MAGNETOSTATICS EXERCISE - BITSAT Archives
8 Videos
- LAWS OF THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - LAWS OF THERMODYNAMICSEXERCISE - 40
1 Videos
- MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONBOOK - BITSAT GUIDECHAPTER - MOTION IN !,2,2 DIMENSIONS AND POJECTILE MOTIONEXERCISE - All Questions
86 Videos
Similar Questions
Knowledge Check
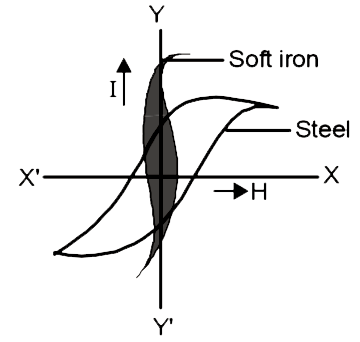
The area enclosed by a hysteresis loop is a measure of
AretentivityBsusceptibilityCpermeabilityDenergy loss per cycleThe area of B-H hysteresis curve is an indication of:
AThe permeability of the substanceBThe susceptibility of the substanceCThe retentivity of the substanceDThe enrgy dissipated per cycle per unit volume of the substanceWhich of the following statement related to the hysteresis loop is incorrect?
AThe curve of B against H for a ferromagnetic material is called hysteresis loopBThe area of B-H curve is a measure of power dissipated per cycle per unit, area of the specimenCCoactivity is a measure of the magnetic field required to destroy the residual magnetism of ferromagnetic materialDThe retentively of a speciment is the measure of magnetic field remaining in the speciment when the magnetising field is removed
The mass of a specimen of a ferromagnetic material is 0.6 kg. and its density is 7.8×103kg/m3. If the area of hysteresis loop of alternating magnetising field of frequency 50Hz is 0.722 MKS units then the hysteresis loss per second will be
View SolutionThe relationship that exists between the electric displacement and the electric field strength in a ferroeleetric is given by the curve of primary polarization and a hysteresis loop. Are there any points on the hysteresis loop to which we might formally assign a dielectric constant equal to zero or to infinity?
View SolutionWhen a ferromagnetic material goes through a hysteresis loop, the magnetic susceptibility
View SolutionWhen a ferromagnetic material goes through a hysteresis loop, the magnetic susceptibility
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
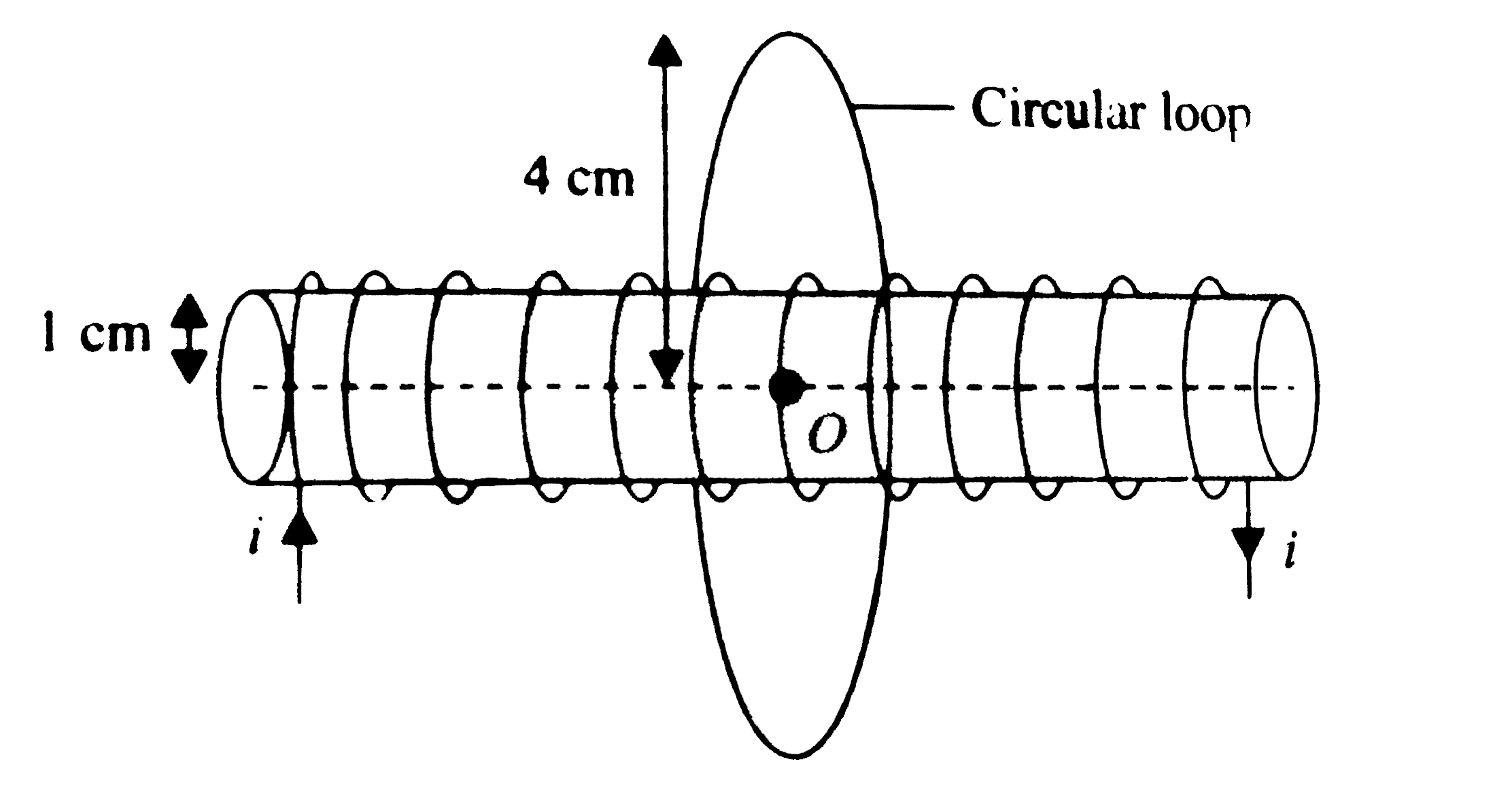
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View Solution
