Question

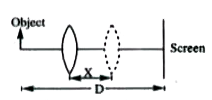
If the distance D between an object and screen than 4 times the focal length of a convex lens, then there are two positions of the lens for which image are formed on the screen. This method is called conjugate method. If d is the distance between the two positions of the lens, obtain the equation for focal length of the convex lens.

Explanation

Let us fix the position of object of object and place the screen to get the enlarged image fist Also, let us fix the position of screen where we get the enlarged image.
Let D be the distance between object and screen. Let us mark the position of lens `d_(1)`. Then let us move the lens away from the object to get a diminished image. Let this position of lens be `d_(2)`. Let d be the distance between the lens position `d_(1) and d_(2)`. Let .v. be the distance b/w image and lens. Let .u. be the distance between object and lens.
From mirror equation.
`(1)/(v) + (1)/(u) = (1)/(f)`
Let us replace v by substituting v = D - u
`(1)/(D-u) + (1)/(u) = (1)/(f)`
we get the equation,`u^(2) - Du + fD = 0`
the quadratic equation for above equation,
`u=(Dpmsqrt(D^(2)-4fD))/(2)`
When D = 4f, we get only position of lens to get image.
This corresponds to placing the object at 2 f and getting the image at 2 f on the otherside.
Hence, for displacement method we need `D gt 4f`. When this condition is satisfied we get
`u_(1)=(D-sqrt(D^(2)-4fD))/(2):"corresponding" " " v_(1) = D-u_(1) = (D-sqrt(D^(2)-4fD))/(2)` after changing the location
`u_(1)=(D-sqrt(D^(2)-4fD))/(2):"corresponding" " " v_(2)=D-u_(2)=(D-sqrt(D^(2)-4fD))/(2)`
now the displacement `d = v_(1) - u_(1)=u_(2)-v_(2)=sqrt(D^(2)-4fD)`
Hence we get focal lenght,
`f = (D^(2) - d^(2))/(4D)`