If the magnetic field at P can be written as Ktan(α2),

A
μ0I4πd
B
μ0I2πd
C
μ0Iπd
D
2μ0Iπd
Video Solution
Text Solution
The correct Answer is:B
(b) 
Let us compute the magnetic field due to any one segment:
B=μ0i4π(dsinα)(cos0∘+cos(180−α))
=μ0I4π(dsinα)(1−cosα)=μ0I4πdtan(α)2
Resultant field will be
Bnet=2B=μ0I2πdtan(α)2⇒K=μ0I2πd
|
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
Knowledge Check
A magnetic field can be produced
Aa moving chargeBa changing electric fieldCboth of theseDneither of theseA magnetic field can be produced
Aa moving chargeBa changing electric fieldCboth of theseDneither of theseA magnetic field can be produced by
Aa moving chargeBa changing electric fieldCboth of theseDneither of these
A proton and an α- particle, having kinetic energies KPandKa respectively enter into a magnetic field at right angles. The ratio of the radii of trajectory of proton to that of α− particle is 2:1. The ratio of Kp:Ka is :
View SolutionA magnetic field can be produced by
View SolutionThe magnetic field at centre , P will be
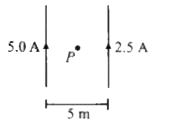
View Solutionp⇒q can also be written as-
View SolutionMetal ring of radius R is placed perpendicular to uniform magnetic field B. Magnetic field starts changing at a rate α
View Solution