If the mass of a spring, m, is not negligible but small compared to the mass M suspended from it, show that the period of oscillations is given by , where k is the force constant of the spring.
[Hint: If x and v be the instaneous displacement and velocity of the lower end, then the displacement of an element at a distance z from the fixed end is xz/l and velocity zv/l. The kinetic energy of the spring =
Total energy of the system = = a constant. Differentiate anmd find T.]
The correct Answer is:NA
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies
39 Videos
- SIMPLE AND COMPOUND PENDULUMBOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise
24 Videos
- SPECIFIC HEAT CAPACITY OF GASESBOOK - NN GHOSHCHAPTER - SPECIFIC HEAT CAPACITY OF GASESEXERCISE - All Questions
17 Videos
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionThe period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
View Solution
Knowledge Check
The period of the free oscillations of the system shown here if mass m1 is pulled down a little and force constant of the spring is k and masses of the fixed pulleys are negligible, is
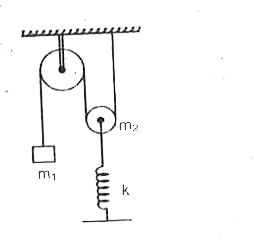 AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2k
AT=2π√m1+m2kBT=2π√m1+4m2kCT=2π√4m1+m2kDT=2π√3m1+m2kWhen a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
A2 secB1 secC4 secD8 secThe period of oscillation of mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
ATBT/√2C2TD√2T
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA mass m is suspended from a spring of force constant k. The period of oscillation is T0 The spring is cut into 4 equal parts: The same mass m is suspended from one of the parts. What is the new period?
View SolutionA body of mass m attached to one end of an ideal spring of force constant k is executing simple harmonic motion. Establish that the time - period of oscillation is T=2π√m/k.
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionThe period of oscilation of a mass M suspended a spring negligible mass is T if along with it and there mass M is also suspended the period of oscillation now be
View Solution
