If the maximum vertical height and horizontal ranges of a projectile are same, the angle of projection will be
45∘
tan−14
tan−12
30∘
The correct Answer is:B
To solve the problem of finding the angle of projection when the maximum vertical height and horizontal range of a projectile are the same, we can follow these steps:
Step 1: Understand the relationships
The maximum height H and the horizontal range R of a projectile launched at an angle θ with an initial velocity u are given by the formulas:
- Maximum height:
H=u2sin2θ2g
- Horizontal range:
R=u2sin2θg
where g is the acceleration due to gravity.
Step 2: Set the equations equal
According to the problem, the maximum height is equal to the horizontal range:
H=R
Substituting the formulas for H and R:
u2sin2θ2g=u2sin2θg
Step 3: Simplify the equation
We can cancel u2 and g from both sides (assuming u≠0 and g≠0):
sin2θ2=sin2θ
Step 4: Use the double angle identity
Recall that sin2θ=2sinθcosθ. Substituting this into the equation gives:
sin2θ2=2sinθcosθ
Step 5: Rearrange the equation
Multiply both sides by 2:
sin2θ=4sinθcosθ
Rearranging gives:
sin2θ−4sinθcosθ=0
Step 6: Factor the equation
Factoring out sinθ:
sinθ(sinθ−4cosθ)=0
This gives us two cases:
1. sinθ=0
2. sinθ−4cosθ=0
Step 7: Solve the first case
For sinθ=0:
- This occurs at θ=0∘ or 180∘, which are not valid angles for projectile motion.
Step 8: Solve the second case
For sinθ−4cosθ=0:
sinθ=4cosθ
Dividing both sides by cosθ gives:
tanθ=4
Thus, we find:
θ=tan−1(4)
Final Answer
The angle of projection θ is:
θ=tan−1(4)
The maximum height H and the horizontal range R of a projectile launched at an angle θ with an initial velocity u are given by the formulas:
- Maximum height:
H=u2sin2θ2g
- Horizontal range:
R=u2sin2θg
where g is the acceleration due to gravity.
According to the problem, the maximum height is equal to the horizontal range:
H=R
Substituting the formulas for H and R:
u2sin2θ2g=u2sin2θg
We can cancel u2 and g from both sides (assuming u≠0 and g≠0):
sin2θ2=sin2θ
Recall that sin2θ=2sinθcosθ. Substituting this into the equation gives:
sin2θ2=2sinθcosθ
Multiply both sides by 2:
sin2θ=4sinθcosθ
Rearranging gives:
sin2θ−4sinθcosθ=0
Factoring out sinθ:
sinθ(sinθ−4cosθ)=0
This gives us two cases:
1. sinθ=0
2. sinθ−4cosθ=0
For sinθ=0:
- This occurs at θ=0∘ or 180∘, which are not valid angles for projectile motion.
For sinθ−4cosθ=0:
sinθ=4cosθ
Dividing both sides by cosθ gives:
tanθ=4
Thus, we find:
θ=tan−1(4)
The angle of projection θ is:
θ=tan−1(4)
Similar Questions
Knowledge Check
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
Atan−1(HR)Btan−1(2HR)Ctan−1(4HR)Dtan−1(4HH)
The horizontal range of a projectile is 2√3 times its maximum height. Find the angle of projection.
View SolutionIn the following questions a statement of assertion (A) is followed by a statement of reason ( R).
A: Horizontal range of a projectile is always same for angle of projection θ with horizontal or θ with vertical .
R : Horizontal range depends only on angle of projection .
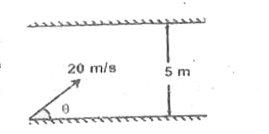
View SolutionA projectile is projected with a speed = 20 m/s from the floor of a 5 m high room as shown. Find the maximum horizontal range of the projectile and the corresponding angle of projection θ.
View SolutionAssertion: In projectile motion, when horizontal range is n times the maximum height, the angle of projection is given by tanθ=4n
Reason: In the case of horizontal projection the vertical increases with time.
View SolutionThe horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
View SolutionThe maximum height attained by a projectile is increased by 5%. Keeping the angle of projection constant, what is the percentage increases in horizontal range?
View Solution(A): The maximum horizontal range of projectile is proportional to square of velocity.
(R): The maximum horizontal range of projectile is equal to maximum height at tained by projectile
View Solution
