if the randon error in the arithmetic mean of 50 observations is α, then the random error in the arithmetic mean of 150 observations would be
α
3α
α3
2α
The correct Answer is:C
To solve the problem, we need to understand how the random error in the arithmetic mean changes with the number of observations.
1. Understanding Random Error: The random error in the arithmetic mean is inversely proportional to the square root of the number of observations. This means that as the number of observations increases, the random error decreases.
2. Given Information: We are given that the random error in the arithmetic mean of 50 observations is denoted as α.
3. Formula for Random Error: The random error (E) in the arithmetic mean can be expressed as:
\(
E = \frac{\sigma}{\sqrt{n}}
\)
where \( \sigma \) is the standard deviation of the observations and \( n \) is the number of observations.
4. Random Error for 50 Observations: For 50 observations, the random error is:
\(
E_{50} = \frac{\sigma}{\sqrt{50}} = \alpha
\)
5. Finding Random Error for 150 Observations: Now, we want to find the random error for 150 observations:
\(
E_{150} = \frac{\sigma}{\sqrt{150}}
\)
6. Relating the Two Errors: We can relate the two errors:
\(
E_{150} = E_{50} \cdot \frac{\sqrt{50}}{\sqrt{150}}
\)
Substituting \( E_{50} = \alpha \):
\(
E_{150} = \alpha \cdot \frac{\sqrt{50}}{\sqrt{150}}
\)
7. Simplifying the Expression: We know that:
\(
\frac{\sqrt{50}}{\sqrt{150}} = \frac{\sqrt{50}}{\sqrt{50 \cdot 3}} = \frac{1}{\sqrt{3}}
\)
Therefore:
\(
E_{150} = \alpha \cdot \frac{1}{\sqrt{3}} = \frac{\alpha}{\sqrt{3}}
\)
8. Final Result: Thus, the random error in the arithmetic mean of 150 observations is:
\(
E_{150} = \frac{\alpha}{\sqrt{3}}
\)
\(
E = \frac{\sigma}{\sqrt{n}}
\)
where \( \sigma \) is the standard deviation of the observations and \( n \) is the number of observations.
\(
E_{50} = \frac{\sigma}{\sqrt{50}} = \alpha
\)
\(
E_{150} = \frac{\sigma}{\sqrt{150}}
\)
\(
E_{150} = E_{50} \cdot \frac{\sqrt{50}}{\sqrt{150}}
\)
Substituting \( E_{50} = \alpha \):
\(
E_{150} = \alpha \cdot \frac{\sqrt{50}}{\sqrt{150}}
\)
\(
\frac{\sqrt{50}}{\sqrt{150}} = \frac{\sqrt{50}}{\sqrt{50 \cdot 3}} = \frac{1}{\sqrt{3}}
\)
Therefore:
\(
E_{150} = \alpha \cdot \frac{1}{\sqrt{3}} = \frac{\alpha}{\sqrt{3}}
\)
\(
E_{150} = \frac{\alpha}{\sqrt{3}}
\)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Assertion and reason15videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Match the column6videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Check Point 1.310videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEYCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason2videos
UNIT AND DIMENSIONS
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
If random error in the arithmetic mean of 100 observations is x, then the randow error in the arithmetic mean of 500 observations would be
A5xBx/5C25xDx/25 - Question 2 - Select One
Find the arithmetic mean of:
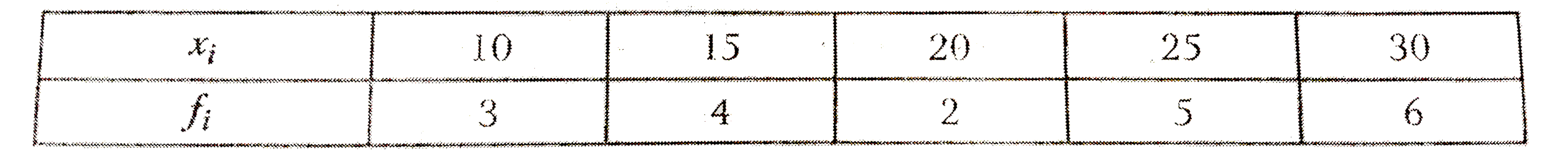 A21B21.4C22.75D21.75
A21B21.4C22.75D21.75
Define Arithmetic mean.
View SolutionDefine Arithmetic mean.
View SolutionSimple Arithmetic Mean
View SolutionWeighted Arithmetic Mean
View SolutionIf arithmetic mean of 9 observations is 100 and that of 6 is 80 .Then the combined mean of all the 15 observations will be
View SolutionIf arithmetic mean of 9 observations is 100 and that of 6 is 80 .Then the combined mean of all the 15 observations will be
View Solution

