If the velocity of an electron is doubled, its de-Broglie frequency will be
half
remain same
doubled
become four times
The correct Answer is:C
To solve the problem of how the de-Broglie frequency changes when the velocity of an electron is doubled, we can follow these steps:
Step 1: Understand the de-Broglie wavelength formula
The de-Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle. For an electron, the momentum p can be expressed as:
p=mv
where m is the mass of the electron and v is its velocity.
Step 2: Relate de-Broglie wavelength to frequency
The de-Broglie frequency (f) can be related to the wavelength and velocity by the equation:
f=vλ
Substituting the expression for λ from Step 1, we get:
f=vhmv=mv2h
Step 3: Analyze the effect of doubling the velocity
If the velocity of the electron is doubled, we can denote the new velocity as v′=2v. Now, substituting v′ into the frequency equation:
f′=m(v′)2h=m(2v)2h=m⋅4v2h=4⋅mv2h=4f
This shows that the new frequency f′ is four times the original frequency f.
Step 4: Conclusion
Thus, if the velocity of the electron is doubled, its de-Broglie frequency will be quadrupled.
Final Answer
The de-Broglie frequency will be 4 times.
---
The de-Broglie wavelength (λ) of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle. For an electron, the momentum p can be expressed as:
p=mv
where m is the mass of the electron and v is its velocity.
The de-Broglie frequency (f) can be related to the wavelength and velocity by the equation:
f=vλ
Substituting the expression for λ from Step 1, we get:
f=vhmv=mv2h
If the velocity of the electron is doubled, we can denote the new velocity as v′=2v. Now, substituting v′ into the frequency equation:
f′=m(v′)2h=m(2v)2h=m⋅4v2h=4⋅mv2h=4f
This shows that the new frequency f′ is four times the original frequency f.
Thus, if the velocity of the electron is doubled, its de-Broglie frequency will be quadrupled.
The de-Broglie frequency will be 4 times.
Topper's Solved these Questions
- CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSBOOK - BITSAT GUIDECHAPTER - CATHODE RAY, PHOTOELECTRIC EFFECT AND X-RAYSEXERCISE - BITSAT Archives
6 Videos
- ATOMIC STRUCTUREBOOK - BITSAT GUIDECHAPTER - ATOMIC STRUCTUREEXERCISE - BITSAT Archives
4 Videos
- CURRENT ELECTRICITYBOOK - BITSAT GUIDECHAPTER - CURRENT ELECTRICITYEXERCISE - Bitsat Archives
26 Videos
Similar Questions
Knowledge Check
When the velocity of an electron increases, its de Broglie wavelength
AincreasesBdecreasesCremains sameDmay increase or decreaseIf the kinetic energy of a free electron doubles , its de - Broglie wavelength changes by the factor
A1√2B√2C12D2The log - log graph between the energy E of an electron and its de - Broglie wavelength λ will be
A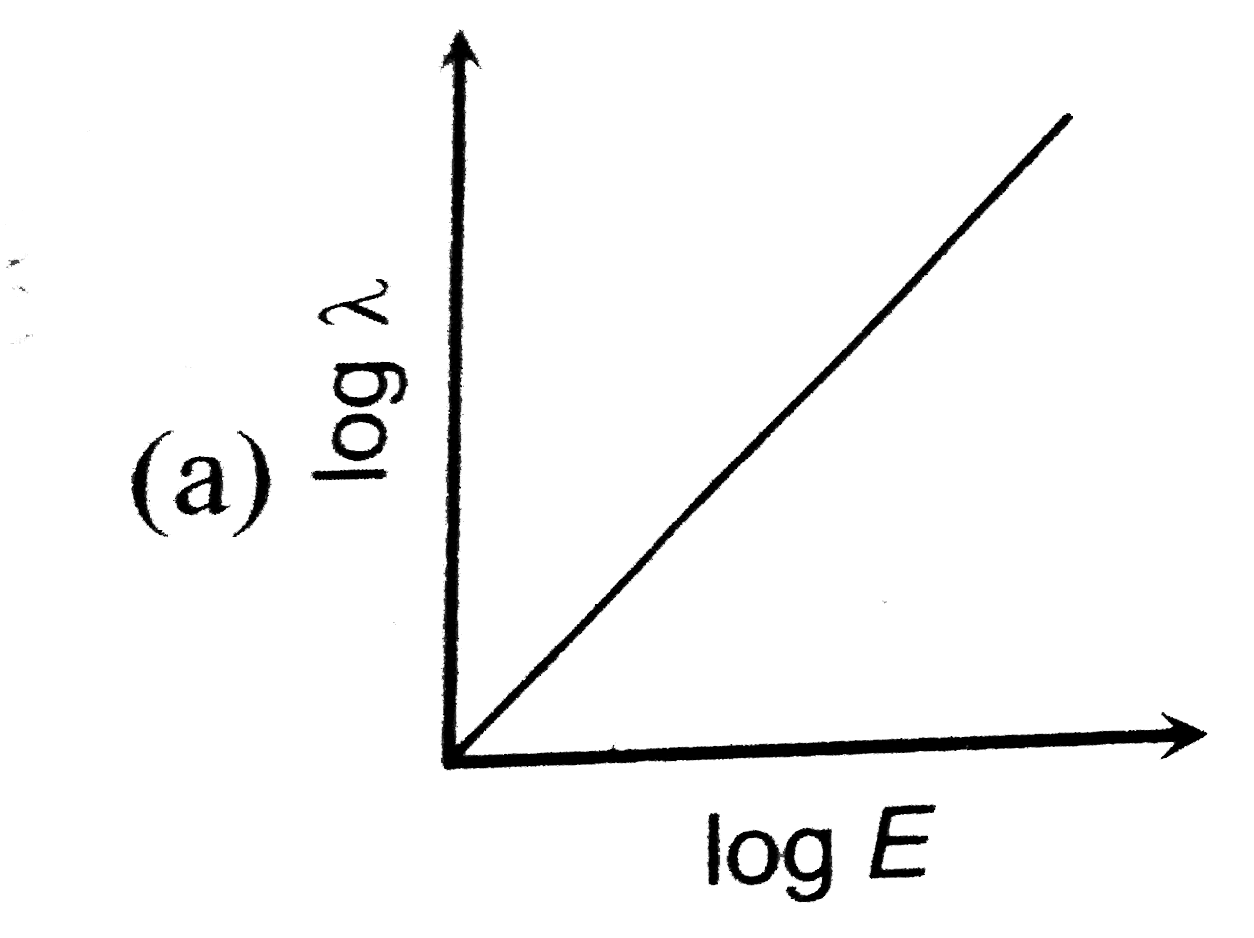 B
B C
C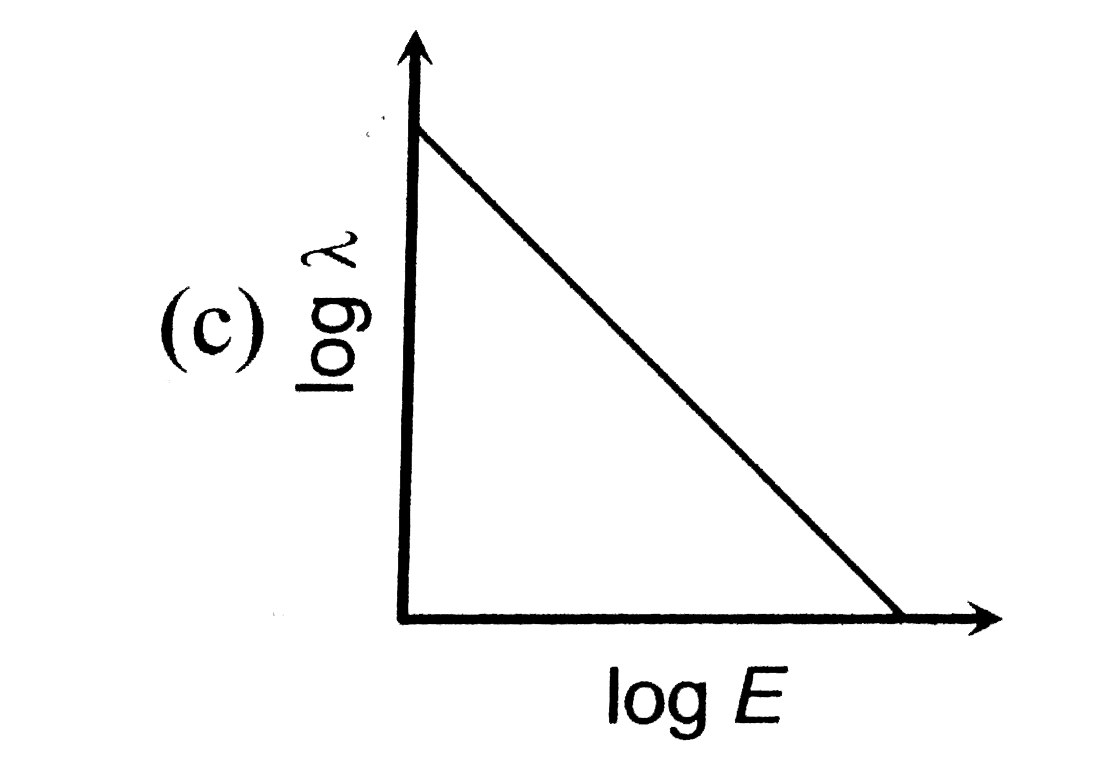 D
D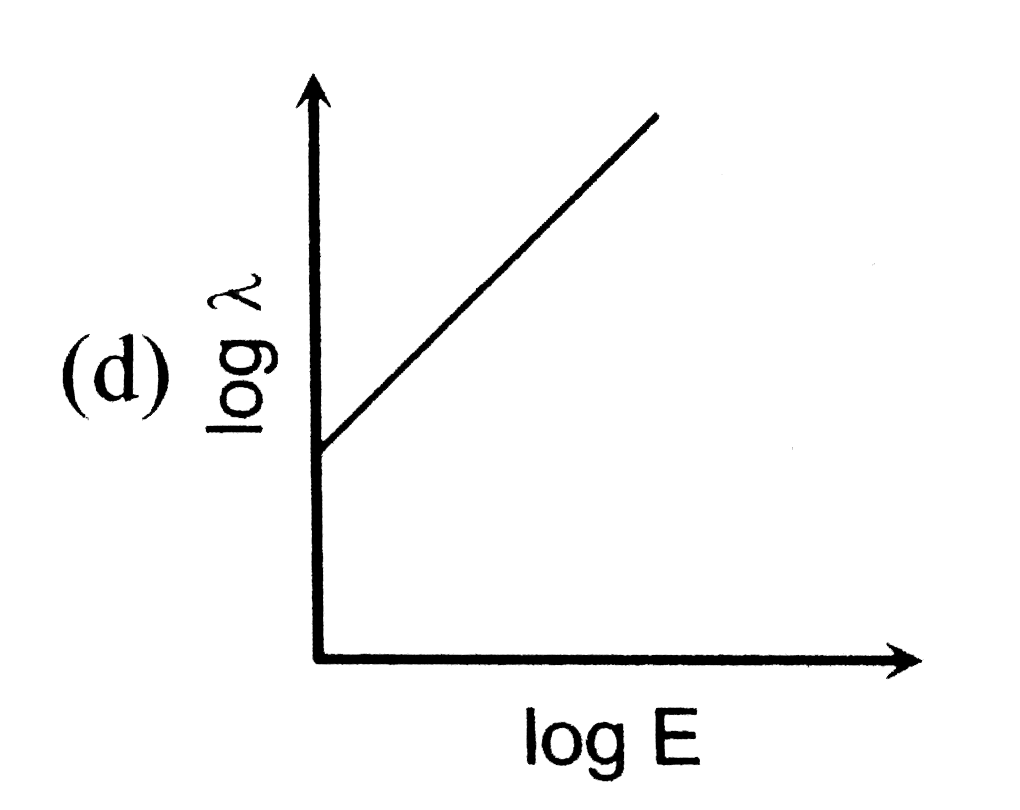
What must be the velocity of a beam of electrons if they are to display a de-Broglie wavelength of 100Å ?
View SolutionWhat must be the velocity of a beam of electron if they are to display a de Broglie wavelength of 1Å
View SolutionIf the kinetic energy of a particle is doubled, de Broglie wavelength becomes:
View SolutionAn electron is moving with the velocity equal to 10% of the velocity of light. Its de-Broglie wave length will be -
View SolutionThe uncertainty in position of an electron in equal to its de Broglie wavelength .The minimum percentage error in de measuremebnt of velocity under this circumstance will be approsimately
View Solution
