Imagine a neutral particle of same mass m as electron revolving around a proton of mass only under newton's gravitational force. Assuming Bohr's quantum condition, the radius of electron orbit is given by:
Step by step video & image solution for Imagine a neutral particle of same mass m as electron revolving around a proton of mass M_(p) only under newton's gravitational force. Assuming Bohr's quantum condition, the radius of electron orbit is given by: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Advance MCQs with One or More Options Correct
30 Videos
- ATOMIC PHYSICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Unsolved Numerical Problems
39 Videos
- ATOMIC PHYSICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Conceptual MCQs Single Option Correct
29 Videos
- CAPACITANCEBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CAPACITANCEEXERCISE - UNSOLVED NUMERICAL PROBLEMS
40 Videos
Similar Questions
Two satellites of mass MA and MB are revolving around a planet of mass M in radius RA and RB respectively. Then?
View SolutionIn a hypothetical concept, electron of mass me revolves around nucleus due to gravitational force of attraction between electron and proton of mass mp. If the radius of circular path of electron is r, then the speed of electron is
View Solution
Knowledge Check
A particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
AGMmRBGMmR2C−GMmR2D0Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmRA satellite of mass m revolves revolves round the earth of mass M in a circular orbit of radius r with an angular velocity ω. If the angular velocity is ω/8 then the radius of the orbit will be
A4rB2rC8rDr
The key feature of Bohr'[s spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton we will extend this to a general rotational motion to find quntized rotantized rotational energy of a diatomic molecule assuming it to be right . The rate to energy applied is Bohr's quantization condition
In a CO molecule, the distance between C(mass=12a.m.u)andO(mass=16a.m.u) where 1 a.m.u = (5)/(3) xx 10^(-27) kg , is close to
View SolutionFour similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by
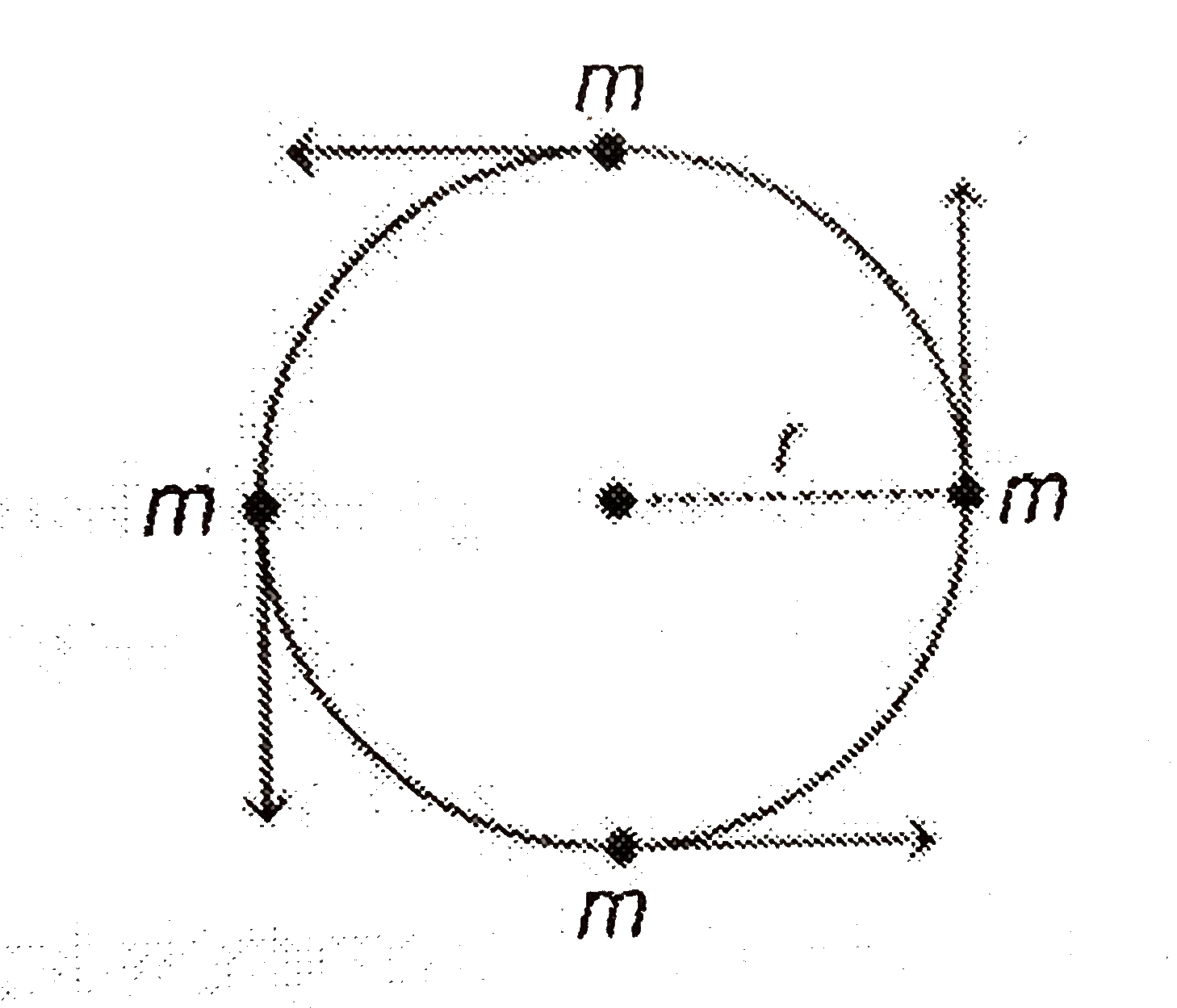
View SolutionThe work done to increases the radius of orbit of a satellite of mass 'm' revolving around a planet of mass M from orbit of radius R into another orbit of radius 3R is
View SolutionTwo point masses M are kept fixed on the x-axis at a distance a from the origin, another point mass m is moving in a circular path of radius R (in y - z plane) under the influence of gravitational force of attraction, then speed of m will be (Assume no forces are acting on m other than the gravitational forces by two M)

View SolutionIf R denotes the radius of orbit of a satellite of mass m revolving around a planet of mass M, the sqiared orbital velocity of the satellite is given by
View Solution
