In a double star, two stars one of mass $m_{1}$ and another of mass $m_{2}$ , with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of eavolution.
(b) the ratio of rheir kintic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

$r_{1} + r_{2} = d$ ..(i)
$m_{1} r_{1} = m_{2} r_{2}$ ..(ii)

Solving these two equations we get,
$r_{1} = (\frac{m_{2}}{m_{1} + m_{2}}) d$ or $r_{2} = (\frac{m_{1}}{m_{1} + m_{2}}) d$
The centripetal force is provided by gravitational firce,
$m_{1} r_{1} ω^{2} = m_{2} r_{2} ω^{2} = \frac{G m_{1} m_{2}}{d^{2}}$
Solving these equations, we get
$ω = \sqrt{\frac{G (m_{1} + m_{2})}{d^{3}}}$
$∴ T = \frac{2 π}{ω} = 2 π \sqrt{\frac{d^{3}}{G (m_{1} + m_{2})}}$
(b) $\frac{K_{1}}{K_{2}} = \frac{\frac{1}{2} I_{1} ω^{2}}{\frac{1}{2} I_{2} ω^{2}} = \frac{I_{1}}{I_{2}} = \frac{m_{1} r_{1}^{2}}{m_{2} r_{2}^{2}}$
$= (\frac{m_{1}}{m_{2}}) {(\frac{r_{1}}{r_{2}})}^{2} = (\frac{m_{1}}{m_{2}}) {(\frac{m_{2}}{m_{1}})}^{2} = \frac{m_{2}}{m_{1}}$
(c ) $\frac{L_{1}}{L_{2}} = \frac{L_{1} ω}{I_{2} ω} = \frac{I_{1}}{I_{2}} = \frac{m_{2}}{m_{1}}$
(d) $L = L_{1} + L_{2} = (I_{1} + L_{2}) ω$
$= (m_{1} r_{1}^{2} + m_{2} r_{2}^{2}) ω$
$= [\frac{m_{1} m_{2}^{2} d^{2}}{{(m_{1} + m_{2})}_{1}^{2}} + \frac{m_{2} m_{1}^{2} d^{2}}{{(m_{1} + m_{2})}_{1}^{2}}] ω$
$= μ ω d^{2}$
where, $μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}} =$ reduced mass
(e) $K = \frac{1}{2} (I_{1} + I_{2}) ω^{2} = \frac{1}{2} μ ω^{2} d^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a double star system one of mass $m_{1}$ and another of mass $m_{2}$ with a separation d rotate about their common centre of mass. Then rate of sweeps of area of star of mass $m_{1}$ to star of mass $m_{2}$ about their common centre of mass is
A $\frac{m_{1}}{m_{2}}$
B $\frac{m_{2}}{m_{1}}$
C $\frac{m_{1}^{2}}{m_{2}^{2}}$
D $\frac{m_{2}^{2}}{m_{1}^{2}}$
Question 2 - Select One

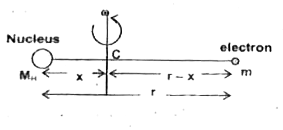
The angular momentum of the atom about the centre of mass will be
A $m r^{2} ω$
B $m {(r - X)}^{2} ω$
C $\frac{(M_{H} + M) r^{2} ω}{M_{H} m^{2}}$
D $\frac{M_{H} m}{M_{H} + m} r^{2} ω$
Question 3 - Select One
Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
A $\frac{1}{2 π} \sqrt{\frac{d^{3}}{3 G m}}$
B $2 π \sqrt{\frac{d^{3}}{3 G m}}$
C $\frac{1}{2 π} \sqrt{\frac{3 G m}{d^{3}}}$
D $2 π \sqrt{\frac{3 G m}{d^{3}}}$

DC PANDEY-GRAVITATION-Level 2 Subjective

Home
Ask Doubt
Profile