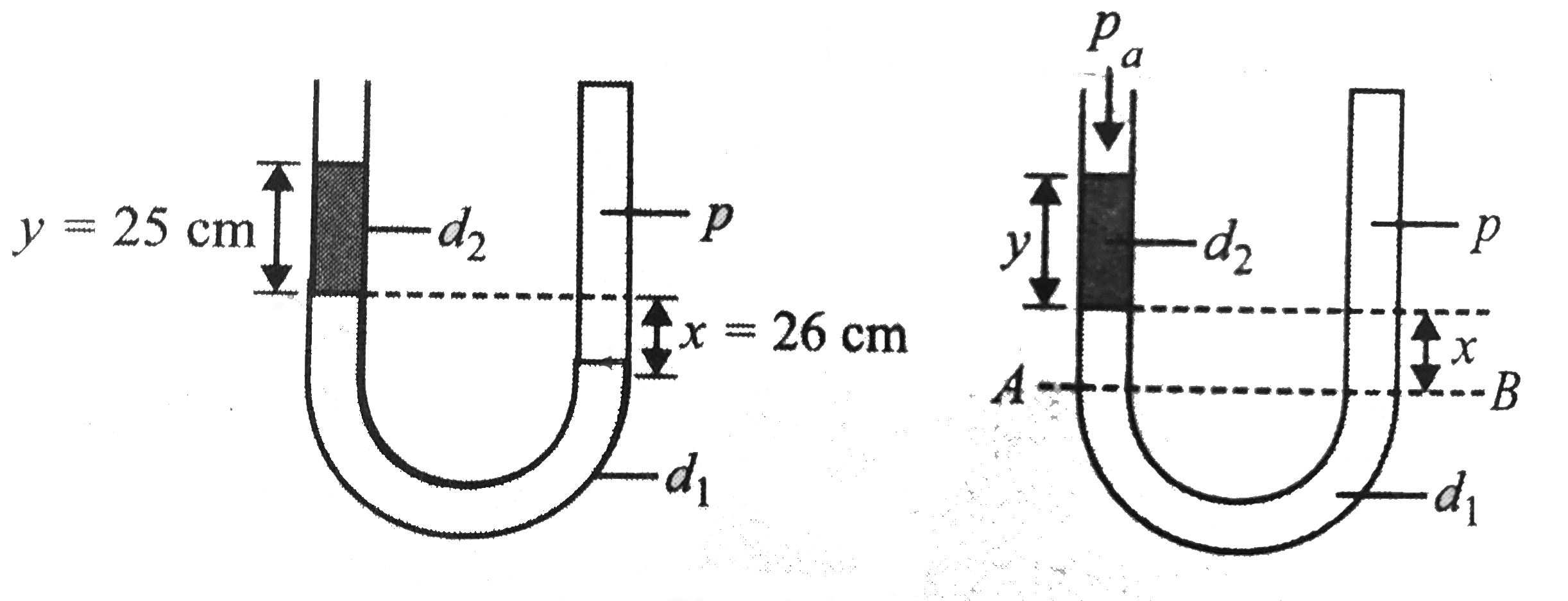
_S01_020_Q01.png)
In a given U-tube (open at one-end) find out relation between p and pa
Given d2=2×13.6gm/cm3,d1=13.6gm/cm3
patm=p
patm=2p
patm=p/2
patm=p/4
The correct Answer is:B
Step by step video, text & image solution for In a given U-tube (open at one-end) find out relation between p and p_(a) Given d_(2)=2xx13.6gm//cm^(3),d_(1)=13.6gm//cm^(3) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Advanced MCQ with one or more options correct
18 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - MCQ
17 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
Similar Questions
Knowledge Check
An ideal gas is collected by downward displacement of water. Select the correct expression for Pgas according to the diagram [dHg=13.6g/cm3]:
 APgas=Patm−[aq. Tension+h13.6]BPgas=Patm−hdgCPgas=Patm+hdgDPgas=Patm−aq. Tension+h13.6
APgas=Patm−[aq. Tension+h13.6]BPgas=Patm−hdgCPgas=Patm+hdgDPgas=Patm−aq. Tension+h13.6The domain of the relation
R={(1,3),(3,5),(2,6)} isA1,3and2B{1,3,2}C{3,5,6}D3,5and6
In the arrangement shown in figure a viscous liquid whose density is 1gm/cm3 flows along a tube out of a wide tank A. Find the velocity of the liquid flow if h1=10cm,h2=20cm,h3=35cm. All the distances l are equal.

View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(B/A)
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(A∩B)
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(A∪B)
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(A/B)
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
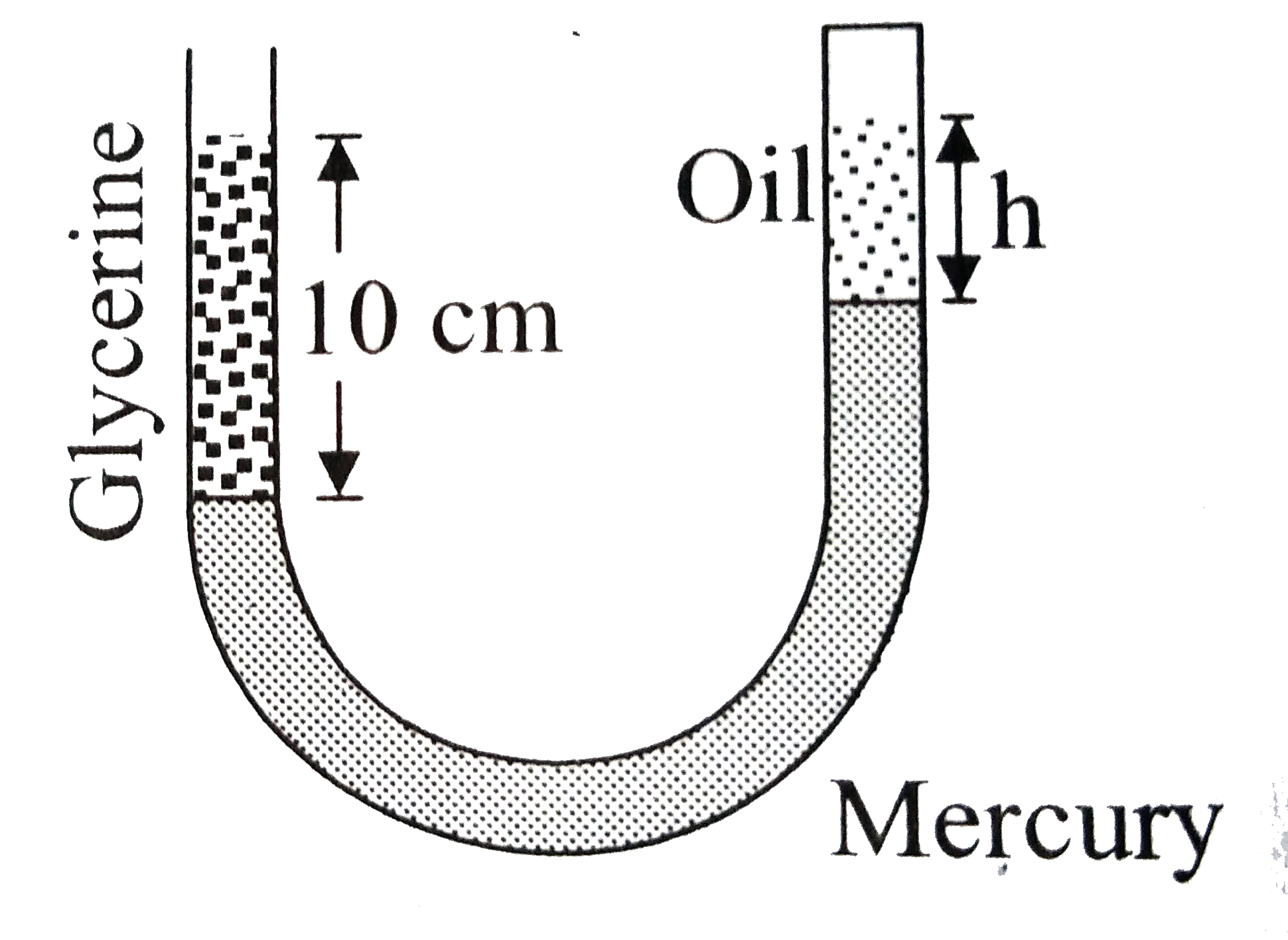
View Solution