In a hydrogen atom, a transition takes place from n = 3 to n = 2 orbit. Calculate the wavelength of the emitted photon. Will the photon be visible ? To which spectral series will this photon belong? Given R=1.097×107m−1
The wavelength of the emitted photon is given by
1λ=R(1n21−132)
When the transition takes place n =3 to n=2, then
1λ=(1.097×107)(122−133)
=1.097×107×436
∴ λ=361.097×107×5=6.563×10−7m
=6563Å
λ falsl in the visible (red) part of the specturm, hence the photon will be visible. This photon is the first member of the Balmar series.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.114videos
ATOMS
- BOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.216videos
ATOMS
- BOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN63videos
ALTERNATING CURRENT
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
Similar Questions
The first excitation potential of sodium atom is 2.1 V. Calculate the longest wavelength of the emitted photon. Will the photon be visible ? To Which spectral series will this photon belong? Given R=1.097×107m−1
View SolutionEnergy level diagram of a hydrogen atom is shown below :
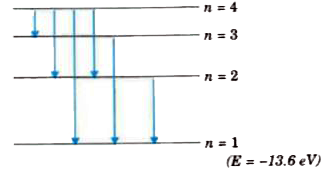
(i)If a transition takes place from n=3 to n=2 orbit, calculate the wavelength of the radiation emitted. Identify the spectral series to which it belongs.
(ii)Which transition results in emission of radiation of maximum wavelength ?View Solution
Knowledge Check
- Question 1 - Select One
In a hydrogen atom, the transition takes place from n = 3 to n = 2 . If Rydberg constant is 1.097×107m−1 , the wavelength of the emitted radiation is
A365RHB5RH36C34RHD43RH - Question 2 - Select One
In hydrogen atom, the transition takes place from n=3 to n=2. If Rydberg's constant is 1.09×10 per metre, the wavelength of the limit emitted is
A6606ÅB4861ÅC4340ÅD4101Å - Question 3 - Select One
In a hydrogen atom, the transition takes place from n=3 to n=2 . If Rydberg constant is 1.097×107m−10. The wavelength of the emiited radiation is
A365RHB5RH36C34RHD43RH
Calculate the wavelength (in nanometers) emitted by a photon during a transition from n =6 to n = 4 state in the H -atom.
View SolutionFind the two longest wavelength (inÅ) emitted when hydrogen atom make transition and the spectrum lines lie in the visible regain (R=1.097×107m−1)
View SolutionIn a hydrogen atom , an electron makes a transition from energy level of -1.51 eV to ground level . Calculate the wavelength of the spectral line emitted and identify the series of hydrogen spectrum to which this wavelength belongs.
View SolutionCalculate the highest frequency of the emitted photon in the Paschen series of spectral lines of the hydrogen atom.
View SolutionIf an electron of a hydrogen atom jumps from n=2 to n=1 then find the wavelength of released photon
View Solution

