In a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
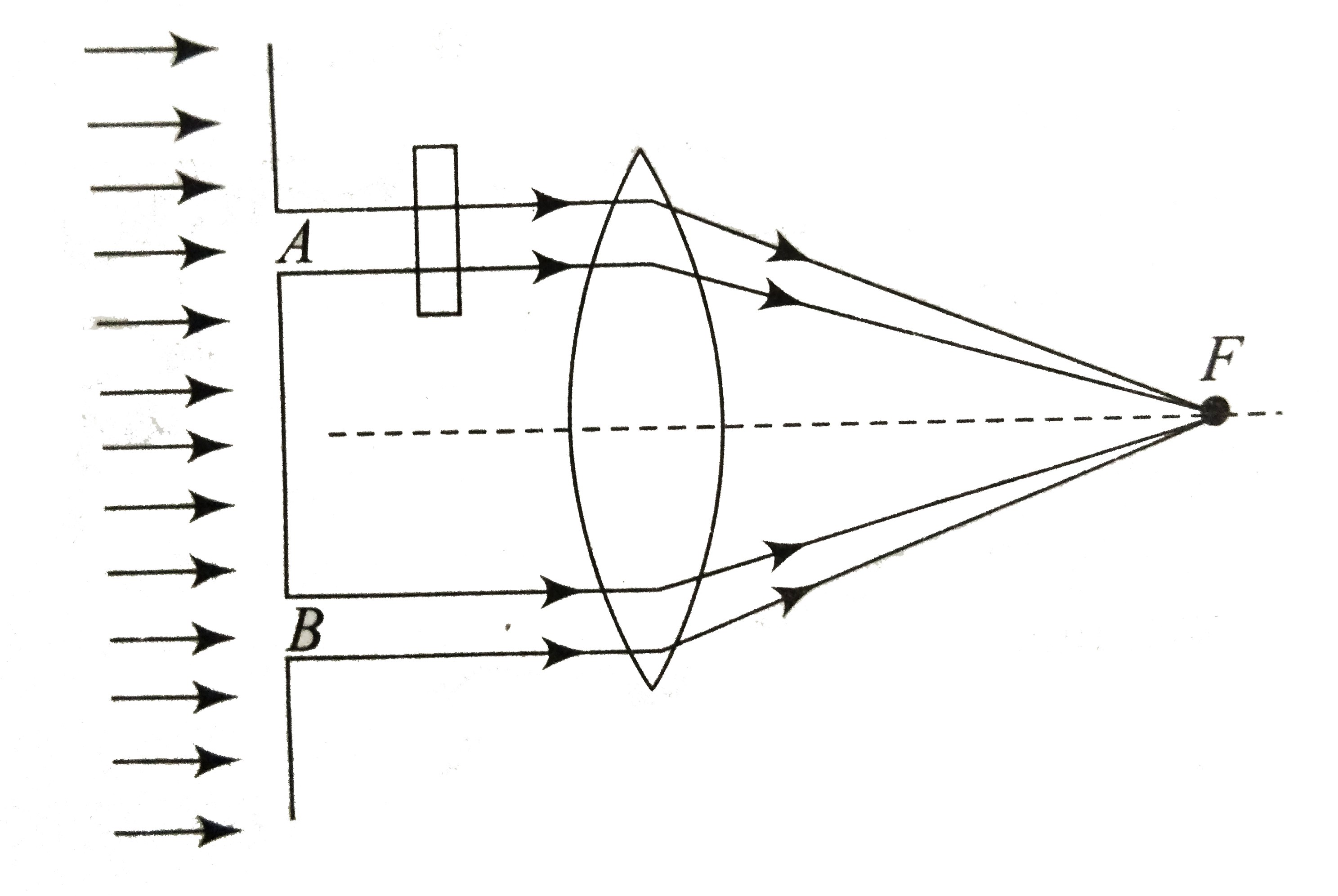
I=10πW/m2
PA=IAA=10π×π(0.001)2=10−5W
PB=IAB=10π×π(0.002)2=4×10−5W
The aperture allows only 10% of power, hence
P′A=0.1×10−5=10−6W
P′B=0.1×4×10−5=4×10−6W
Film: t=200nm,μ=3/2,λ=600nm
Path difference due ti film,
Δx=(μ−1)t=(3/2−1)×200=100nm
Phase difference ϕ=2πλΔx=2π600×100=π3
Power received at F
P=P′A+P′B+2√P′A−P′Bcosϕ
=10−6+4×10−6+2√10−6×4×10−6cos(π/3)
=10−6+4×10−6+2×10−6
=7×10−6W
Topper's Solved these Questions
Similar Questions
In a modified Young's double slit experiment a monochromatic uniform and parallel beam of light of wave length 6000Å and intensity (10π)Wm−2 is incident normally on two circular apertures A and B of radii 20009Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture. A. Calculate the power (in watt) received at the focal spot F of the lens. The lens is symmertrically placed with respect to the apertures. Assume that 10% of the power received by each aperture goes in the originally direction and is brought to the focal spot.
 View Solution
View SolutionIn a Young's experiment , the slits are 1.5 m from the screen . The width of the fringes observed with light of wavelength 6000 Å is 1.0 nm . What is the separation of the slits .
View Solution
Knowledge Check
- Question 1 - Select One
A light has a wavelength 6000Å. The energy of this light is
A5eVB2.07eVC1.07eVD0.207eV - Question 2 - Select One
In Young's experiment , the fringe width of the fringes with light of wavelength 6000 Å is 2.0 mm . What will be the fringe width if the entire apparatus is immersed in a liquid of refractive index 1.33 ?
A5mmB3mmC1.5mmD1mm - Question 3 - Select One
In young's double slit experiment, the two slits are 0.2 mm apart. The fringes for light of wavelength 6000Å are found on the screen 80 cm away. The distance of fifth dark fringe, from the central fringe, will be
A6.8 mmB7.8 mmC9.8 mmD10.8 mm
A parallel beam of light of wavelength 6000Å gets diffracted by a single slit of width 0.3 mm. The angular position of the first minima of diffracted light is :
View SolutionIn Young's double slit experiment, the fringe width obtained by a monochromatic light of wavelength 6000Å is 2 mm. I fthe apparatus is dipped into water of R.I. 1:33, then change in fringe width will be
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
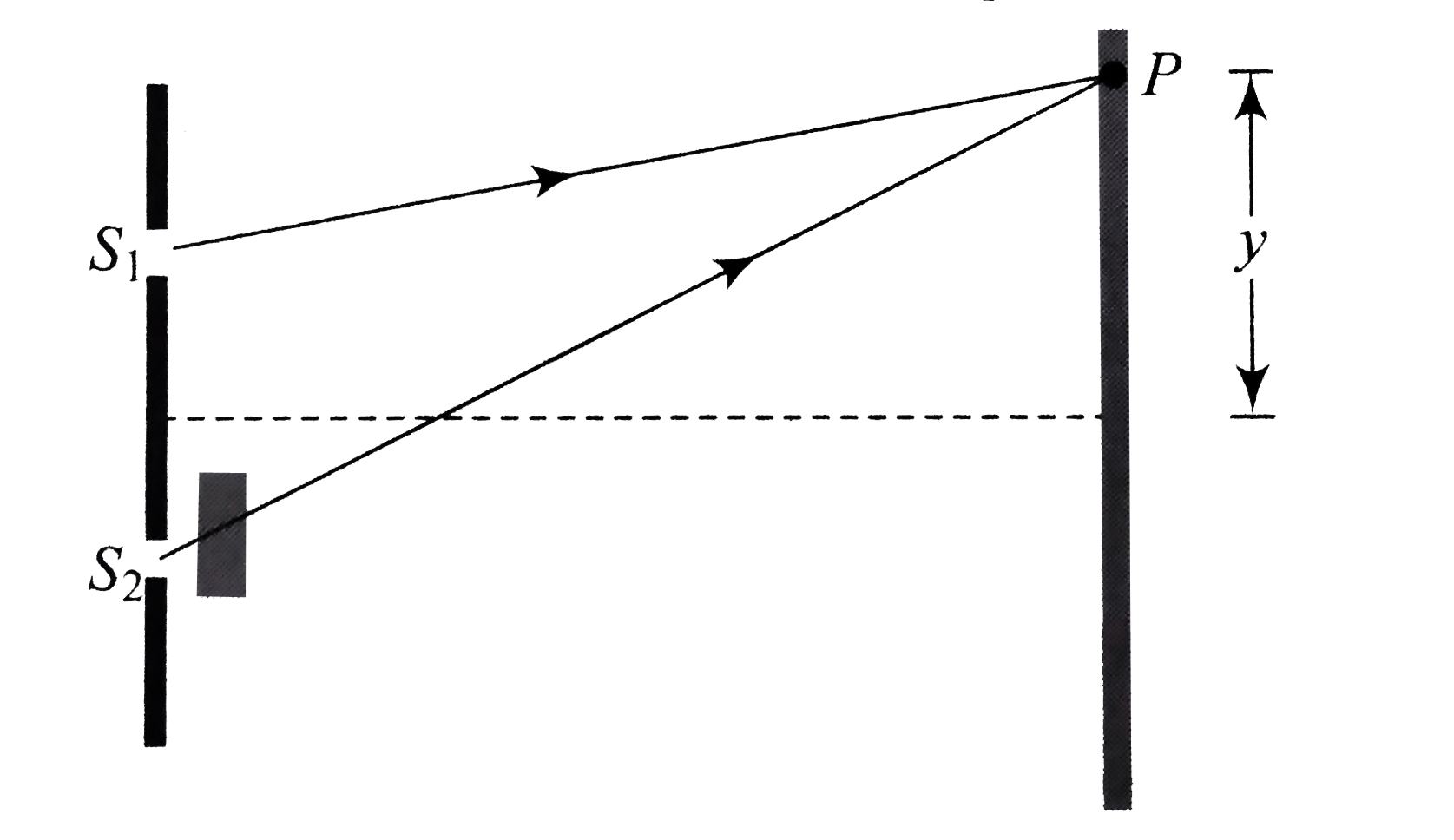
The value of η isView SolutionIn Young's double slit experiment, we get 60 fringes in the field of view of monochromatic light of wavelength 4000Å. If we use monochromatic light of wavelength 6000Å, then the number of fringes obtained in the same field of view is
View SolutionWhen a transparent film of refractive index 1.5 is kept over one of the openings of a double slit experiment apparatus, the interference pattern is shifted through six successive maxima, towards the side, where the film was placed. What is the thickness of the film if the wavelength of light used in 6000 Å?
View Solution

