In a p-V diagram for an ideal gas (Where , p is along y-axis and V is

For a p-V plot, the slope of an adiabatic curve = x × slope of isothermal at the same point. Here x is :
A $\frac{R}{λ - 1}$
B $\frac{1}{λ}$
C $λ$
D $\frac{1}{λ - 1}$
Representing the stopping potential V along X - axis and $\frac{1}{λ}$ along Y - axis for a given photocathode , slope of curve for photoelectric effect is
A $\frac{n c}{e}$
B $\frac{h e}{c}$
C $\frac{e}{h c}$
D $\frac{c}{ne}$
In the following P–V diagram of an ideal gas, two adiabates cut two isotherms at $T_{1}$ and $T_{2}$ The value of $V_{B} / V_{C}$ is :

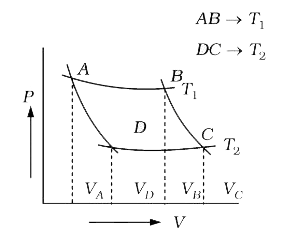A $= V_{A} / V_{D}$
B $< V_{A} / V_{D}$
C $> V_{A} / V_{D}$
Dcannot say

In a p-V diagram for an ideal gas (Where , p is along y-axis and V is along X- axis) , the value of the ratio "slope pof adiabatic curve/ Slope of the isothermal curve"at any point will be (Where symbols have their usual meanings ).