In a process V∝T2, temperature of 2 moles of a gas is increased by 200K. Work done by the gas in this process will be
600 R
800 R
1000 R
1200 R
The correct Answer is:B
To solve the problem of finding the work done by the gas in the process where volume V is proportional to T2, we can follow these steps:
Step 1: Understand the relationship between volume and temperature
Given that V∝T2, we can express this as:
V=kT2
where k is a constant.
Step 2: Use the ideal gas law
From the ideal gas law, we know:
PV=nRT
Substituting V from the previous step, we get:
P(kT2)=nRT
This simplifies to:
P=nRk⋅1T
Step 3: Identify the polytropic process
In this case, since V∝T2, we can identify that this is a polytropic process with γ=12.
Step 4: Use the work done formula for a polytropic process
The work done W in a polytropic process is given by:
W=nRΔT1−γ
where n is the number of moles, R is the gas constant, ΔT is the change in temperature, and γ is the polytropic index.
Step 5: Substitute the values
From the problem, we have:
- n=2 moles
- ΔT=200K
- γ=12
Substituting these values into the work done formula:
W=2R⋅2001−12
W=400R0.5
W=800R
Step 6: Conclusion
Thus, the work done by the gas in this process is:
W=800R
Given that V∝T2, we can express this as:
V=kT2
where k is a constant.
From the ideal gas law, we know:
PV=nRT
Substituting V from the previous step, we get:
P(kT2)=nRT
This simplifies to:
P=nRk⋅1T
In this case, since V∝T2, we can identify that this is a polytropic process with γ=12.
The work done W in a polytropic process is given by:
W=nRΔT1−γ
where n is the number of moles, R is the gas constant, ΔT is the change in temperature, and γ is the polytropic index.
From the problem, we have:
- n=2 moles
- ΔT=200K
- γ=12
W=2R⋅2001−12
W=400R0.5
W=800R
Thus, the work done by the gas in this process is:
W=800R
Topper's Solved these Questions
Similar Questions
At 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
(c) the work done by the gas during the process. [ R=8.31J/mol−K]
View SolutionMethod 1 of Q
Temperature of two moles of a monoatomic gas is increased by 300 K in the process p∝V.
(a) Find molar heat capacity of the gas in the given process.
(b) Find heat given to the gas in that.
View Solution
Knowledge Check
Assertion: In the process pT=constant, if temperature of gas is increased work done by the gas is positive.
Reason: For the given process, V∝T.A(a) If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.B(b) If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.C(c) If Assertion is true, but the Reason is false.D(d) If Assertion is false but the Reason is true.In the process pV2= constant, if temperature of gas is increased, then
A(a) change in internal energy of gas is positiveB(b) work done by gas is positiveC(c) heat is given to the gasD(d) heat is taken out from the gasOne mole of an ideal monoatomic gas under goes a process V=aT2. The temperature of the gas increases by 100K. Which of the following is incorrect ?
Athe work done by the gas in the process is 200R JouleBthe molar heat capacity for the process is 7R2Cfor the process PT2= constantDfor the process coefficient of volume expansion is γ=2T
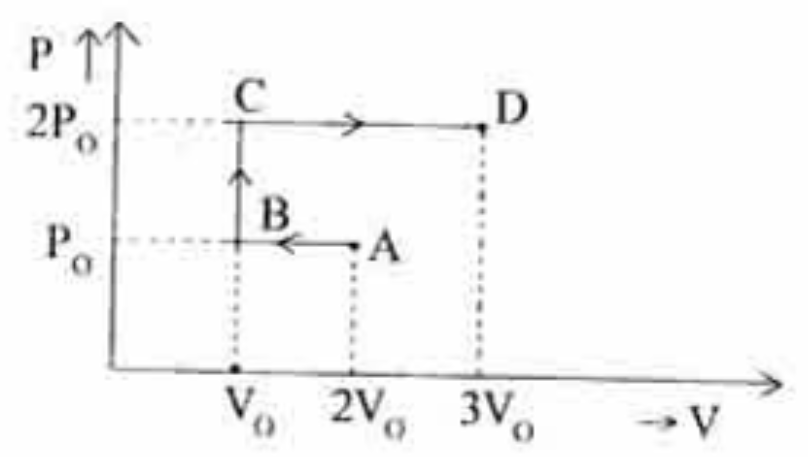
The work done by the gas in the process shown in given P-V diagram is
View SolutionIn a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
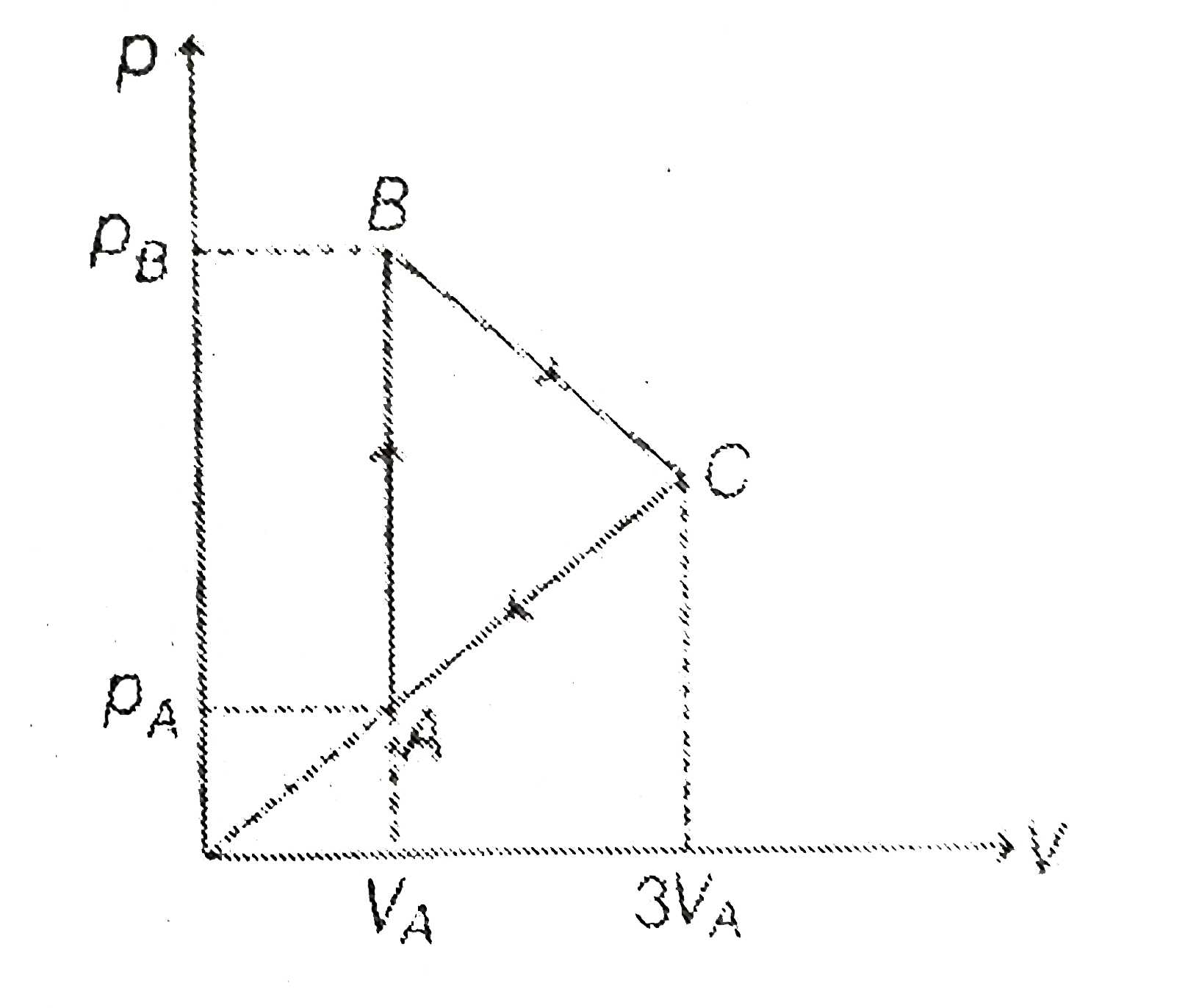
Net work done by the gas in the process is
View SolutionAssertion: In a thermodynamic process, initial volume of gas is equal to final volume of gas. Work done by gas in this process should be zero
Reason: Work done by gas in isochoric process is zero.
View SolutionIf a pari of inear equations is consistent then the lines represented by then are
View Solution
