In a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
can not be a circle
may be a circle
may be a straight line
may be a helix
The correct Answer is:a,c,d
To analyze the path of a charged particle in a region where both a non-zero uniform electric field and a magnetic field coexist, we can break down the problem step by step.
1. Identify the Forces Acting on the Charged Particle:
- A charged particle in an electric field experiences an electric force given by →FE=q→E, where q is the charge and →E is the electric field.
- The particle also experiences a magnetic force given by →FB=q(→v×→B), where →v is the velocity of the particle and →B is the magnetic field.
2. Determine the Nature of the Forces:
- The electric force acts in the direction of the electric field.
- The magnetic force acts perpendicular to both the velocity of the particle and the magnetic field direction due to the cross product nature of the magnetic force.
3. Analyze the Possibility of Circular Motion:
- For a charged particle to move in a circular path, a net centripetal force must act towards the center of the circular path.
- In a uniform electric field, the electric force will not provide a centripetal force but will instead push the particle in the direction of the field.
4. Consider Different Scenarios:
- If the electric and magnetic forces balance each other, the net force could be zero, leading to uniform motion in a straight line.
- If the particle's velocity is perpendicular to the magnetic field and the electric field, it could spiral or move in a helical path due to the continuous change in direction caused by the magnetic force.
5. Conclusion on Possible Paths:
- The path of the charged particle cannot be a perfect circle due to the presence of the electric force.
- The particle may move in a straight line if forces balance or in a helical path if the forces do not balance but are perpendicular.
Final Answer:
The path of a charged particle in a region with both a non-zero uniform electric field and a magnetic field can be a straight line or a helix, but it cannot be a circular path.
- A charged particle in an electric field experiences an electric force given by →FE=q→E, where q is the charge and →E is the electric field.
- The particle also experiences a magnetic force given by →FB=q(→v×→B), where →v is the velocity of the particle and →B is the magnetic field.
- The electric force acts in the direction of the electric field.
- The magnetic force acts perpendicular to both the velocity of the particle and the magnetic field direction due to the cross product nature of the magnetic force.
- For a charged particle to move in a circular path, a net centripetal force must act towards the center of the circular path.
- In a uniform electric field, the electric force will not provide a centripetal force but will instead push the particle in the direction of the field.
- If the electric and magnetic forces balance each other, the net force could be zero, leading to uniform motion in a straight line.
- If the particle's velocity is perpendicular to the magnetic field and the electric field, it could spiral or move in a helical path due to the continuous change in direction caused by the magnetic force.
- The path of the charged particle cannot be a perfect circle due to the presence of the electric force.
- The particle may move in a straight line if forces balance or in a helical path if the forces do not balance but are perpendicular.
The path of a charged particle in a region with both a non-zero uniform electric field and a magnetic field can be a straight line or a helix, but it cannot be a circular path.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Matrix Matching type Questions
12 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
View SolutionA charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other . The particle will remove in a
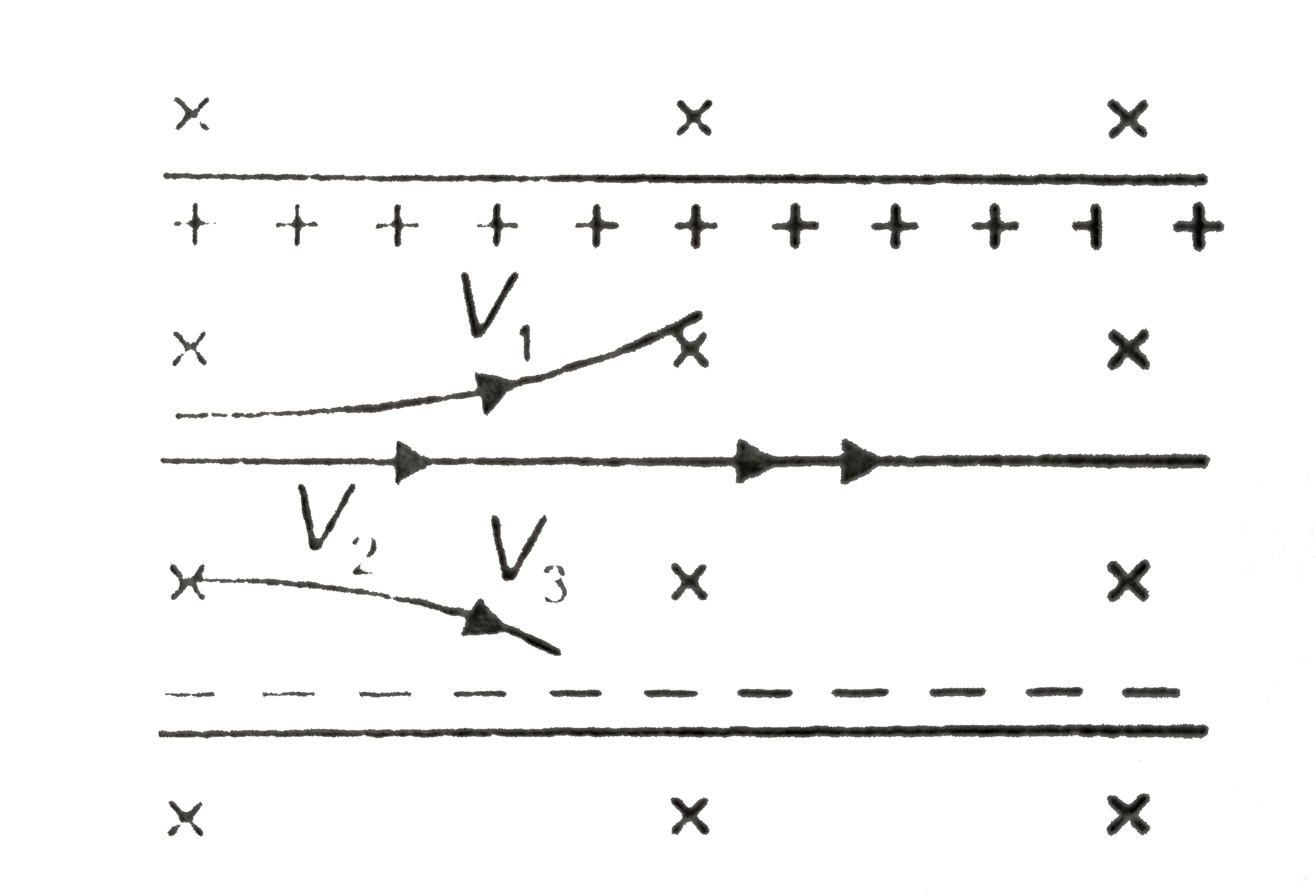
View SolutionIn a region of crossed fields as shown, the strength of electric field is E and that of magnetic field is B. Three positively charged particles with speeds V1,V2andV3 are projected and their paths are shown. From this it implies that
View SolutionStatement-1 In a region of space, both electric and magnetic field act in same direction. When a charged particle is projected parallel to fields, it moves undeviated
Statement-2 Here, net force on the particle is not zero
View SolutionA charge q moves region in a electric field E and the magnetic field B both exist, then the force on its is
View SolutionIn a region, steady and uniform electric and magnetic fields are present . These two fields are parallel to each other. A charged particle is released from rest in this region . The path of the particle will be a
View SolutionA charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
View SolutionAssertion If the path of a charged particle in a region of uniform electric and magnetic field is not a circle, then its kinetic energy may remain constant.
Reason In a combined electric and magnetic field region a moving charge experiences a net force
F=qE+q(V×B), where symbols have their usual meanings.
View Solution
