In a Rutherford scattering experiment, assume that an incident alpha particle (radius 1.80 fm) is headed directly toward a target gold nucleus (radius 6.23 fm). What energy must the alpha particle have to just barely "touch" the gold nucleus?
The correct Answer is:28.3×106eV
To solve the problem of determining the energy that an alpha particle must have to just barely touch a gold nucleus, we will use the concept of electrostatic potential energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Situation
An alpha particle is a helium nucleus consisting of 2 protons and 2 neutrons, and it is positively charged. The gold nucleus has an atomic number of 79, meaning it has 79 protons and is also positively charged. When the alpha particle approaches the gold nucleus, they will repel each other due to their positive charges.
Step 2: Determine the Charges
- The charge of the alpha particle (Q1) is:
Q1=2e=2×1.6×10−19C=3.2×10−19C
- The charge of the gold nucleus (Q2) is:
Q2=79e=79×1.6×10−19C=1.264×10−17C
Step 3: Calculate the Distance Between the Centers
The distance R between the centers of the alpha particle and the gold nucleus is the sum of their radii:
R=Ralpha+Rgold=1.80fm+6.23fm=8.03fm=8.03×10−15m
Step 4: Use the Formula for Electrostatic Potential Energy
The electrostatic potential energy (U) at the distance R is given by:
U=14πϵ0Q1Q2R
Where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
Step 5: Substitute the Values
Substituting the values into the formula:
U=14π(8.85×10−12)(3.2×10−19)(1.264×10−17)8.03×10−15
Calculating 14πϵ0:
14πϵ0≈9×109N m2/C2
Now substituting:
U≈9×109×(3.2×10−19)(1.264×10−17)8.03×10−15
Step 6: Calculate the Result
Calculating the numerator:
(3.2×10−19)(1.264×10−17)≈4.038×10−36
Now calculating U:
U≈9×109×4.038×10−368.03×10−15≈4.52×10−11J
Step 7: Convert to Electron Volts
To convert joules to electron volts:
1eV=1.6×10−19J
Thus,
U≈4.52×10−111.6×10−19≈282.5MeV
Final Answer
The energy that the alpha particle must have to just barely touch the gold nucleus is approximately 282.5 MeV.
---
An alpha particle is a helium nucleus consisting of 2 protons and 2 neutrons, and it is positively charged. The gold nucleus has an atomic number of 79, meaning it has 79 protons and is also positively charged. When the alpha particle approaches the gold nucleus, they will repel each other due to their positive charges.
- The charge of the alpha particle (Q1) is:
Q1=2e=2×1.6×10−19C=3.2×10−19C
- The charge of the gold nucleus (Q2) is:
Q2=79e=79×1.6×10−19C=1.264×10−17C
The distance R between the centers of the alpha particle and the gold nucleus is the sum of their radii:
R=Ralpha+Rgold=1.80fm+6.23fm=8.03fm=8.03×10−15m
The electrostatic potential energy (U) at the distance R is given by:
U=14πϵ0Q1Q2R
Where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
Substituting the values into the formula:
U=14π(8.85×10−12)(3.2×10−19)(1.264×10−17)8.03×10−15
14πϵ0≈9×109N m2/C2
U≈9×109×(3.2×10−19)(1.264×10−17)8.03×10−15
Calculating the numerator:
(3.2×10−19)(1.264×10−17)≈4.038×10−36
Now calculating U:
U≈9×109×4.038×10−368.03×10−15≈4.52×10−11J
To convert joules to electron volts:
1eV=1.6×10−19J
Thus,
U≈4.52×10−111.6×10−19≈282.5MeV
The energy that the alpha particle must have to just barely touch the gold nucleus is approximately 282.5 MeV.
Topper's Solved these Questions
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
69 Videos
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
22 Videos
- THE NUCLEUSBOOK - RESNICK AND HALLIDAYCHAPTER - THE NUCLEUSEXERCISE - CHECKPOINT
5 Videos
- THE KINETIC THEORY OF GASESBOOK - RESNICK AND HALLIDAYCHAPTER - THE KINETIC THEORY OF GASESEXERCISE - PRACTICE QUESTIONS
72 Videos
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
11 Videos
Similar Questions
Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:

(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionRutherford's alpha particle scattering experiment on thin gold foil was responsible for the discovery of
View Solution
Knowledge Check
In Rutherford's gold foil experiment, the scattering of α-particles takes place. In this process:
Acoulombic force is involvedBnuclear force is involvedCpath of α-particle is parabolicDpath of α-particle is hyperbolicIn Rutherford's scattering experiment of α-particles by metallic foils, with the increase of atomic number of nucleus, the scattering angle .
ARemains unchargedBDecreasesCIncreasesDNone of theseRead the following passage carefully and answer the questions
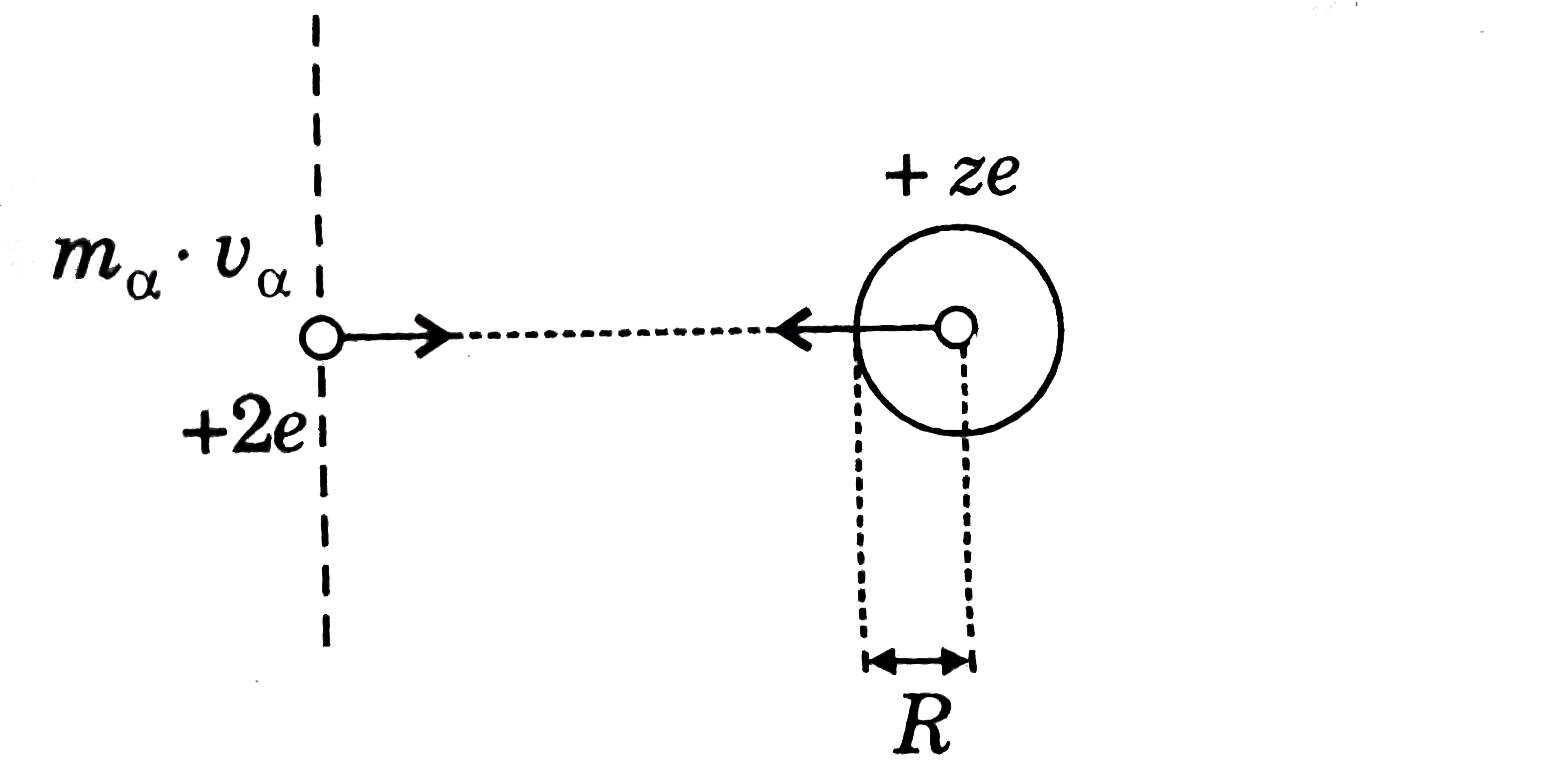
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of α−particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , α−particle with half of the earlier speed then the percentage error involved in the radius calculation is :A0.75B1C3D4
In a head on collision between an alpha particle and gold nucleus (Z=79), the distance of closest approach is 39.5 fermi. Calculate the energy of α-particle.
View SolutionCalculate the energy of an α-particle whose distance of closest approach with the gold nucleus is 29.5 fermi.
View SolutionIn Rutherford α-sattering experiment , the ratio of number of particles scattered at an angle of 180∘ to the number of particles scattered at an angle of 90∘ is α:4. What is the value of α ?
View SolutionRead the following passage carefully and answer the questions
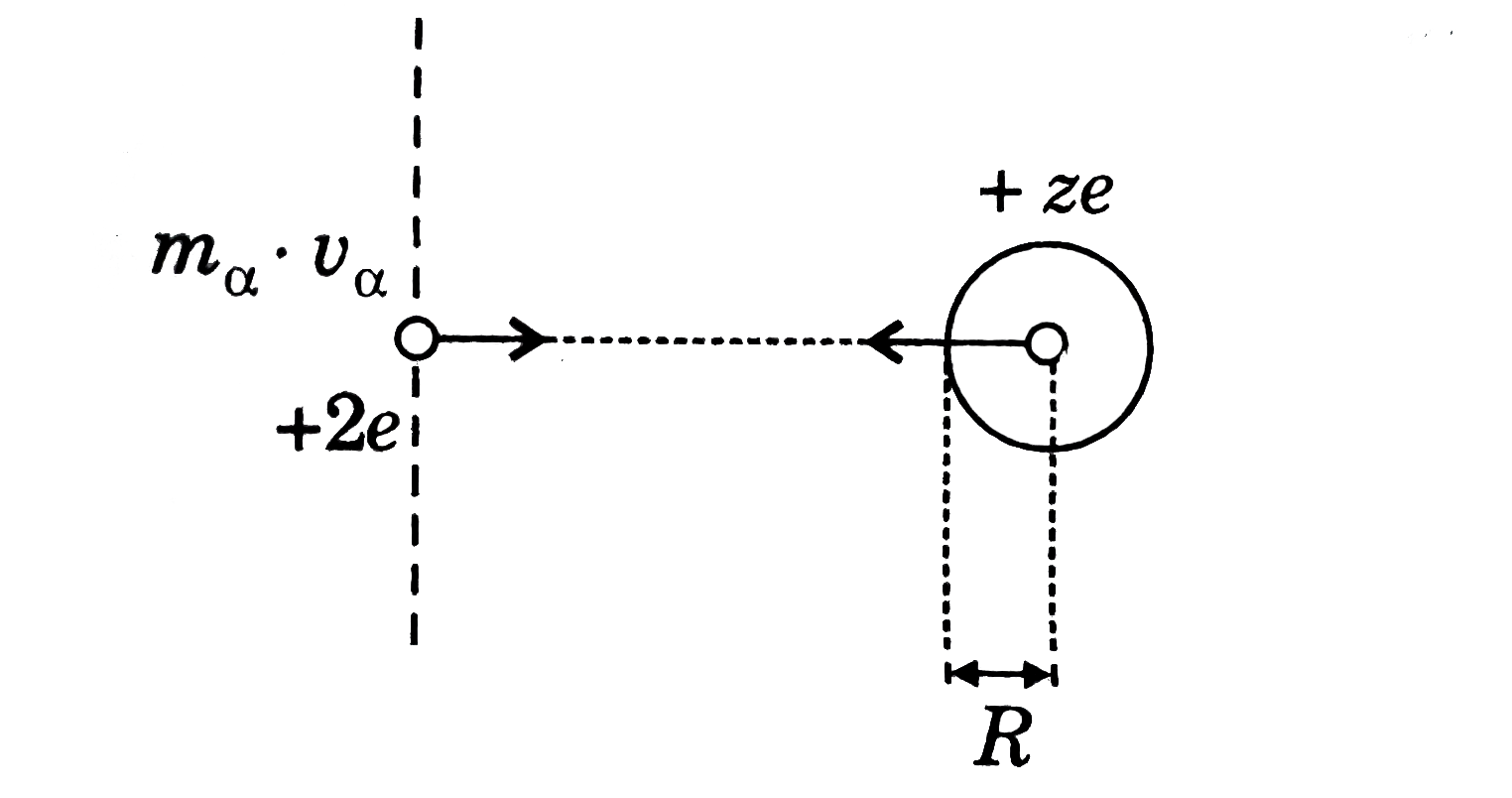
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
If α−particle with speed v0 is projected from infinity and it approaches upto r0 distance from the nuclei. Then the speed of α−particle which approaches 2r0 distance from the nucleus is
View SolutionIn Geiger marsden experiment in a head on collision between an α particles and a gold nucleus the minimum separation is 4×10−14 m . the energy of α particle is
View Solution
