In a series LCR circuit, the frequencies at which the current amplitude ismes the current amplitude at resonance are Find the frequency bandwidth of resonance which is defined as Express your answer in terms of R and L. Assume that resonance frequency
The correct Answer is:
To solve the problem of finding the frequency bandwidth of resonance in a series LCR circuit, we will follow these steps:
Step 1: Identify the Resonance Frequency
The resonance frequency f0 for a series LCR circuit is given by the formula:
f0=12π√LC
Step 2: Write the Expression for Current Amplitude
The current amplitude I at a frequency f is given by:
I=V0Z
where Z is the impedance of the circuit. The impedance Z for a series LCR circuit is:
Z=√R2+(ωL−1ωC)2
Here, ω=2πf.
Step 3: Set Up the Condition for Current Amplitude
At the frequencies f1 and f2, the current amplitude is given as:
I=V0Z=1√2⋅V0R
This leads to:
Z=√2R
Thus, we have:
R2+(ωL−1ωC)2=2R2
This simplifies to:
(ωL−1ωC)2=R2
Step 4: Solve for Frequencies f1 and f2
Taking the square root gives us two equations:
1. ωL−1ωC=R
2. ωL−1ωC=−R
For f1:
2πf1L−12πf1C=R(Equation 1)
For f2:
2πf2L−12πf2C=−R(Equation 2)
Step 5: Manipulate the Equations
From Equation 1:
2πf1L=R+12πf1C
From Equation 2:
2πf2L=−R+12πf2C
Step 6: Find the Bandwidth Δf
To find the bandwidth Δf=f2−f1, we can use the relationships derived from the equations. By manipulating the equations and using the approximation f0≫Δf, we can derive:
Δf=R2πL
Final Answer
Thus, the frequency bandwidth of resonance Δf is given by:
Δf=R2πL
The resonance frequency f0 for a series LCR circuit is given by the formula:
f0=12π√LC
The current amplitude I at a frequency f is given by:
I=V0Z
where Z is the impedance of the circuit. The impedance Z for a series LCR circuit is:
Z=√R2+(ωL−1ωC)2
Here, ω=2πf.
At the frequencies f1 and f2, the current amplitude is given as:
I=V0Z=1√2⋅V0R
This leads to:
Z=√2R
Thus, we have:
R2+(ωL−1ωC)2=2R2
This simplifies to:
(ωL−1ωC)2=R2
Taking the square root gives us two equations:
1. ωL−1ωC=R
2. ωL−1ωC=−R
2πf1L−12πf1C=R(Equation 1)
For f2:
2πf2L−12πf2C=−R(Equation 2)
From Equation 1:
2πf1L=R+12πf1C
From Equation 2:
2πf2L=−R+12πf2C
To find the bandwidth Δf=f2−f1, we can use the relationships derived from the equations. By manipulating the equations and using the approximation f0≫Δf, we can derive:
Δf=R2πL
Thus, the frequency bandwidth of resonance Δf is given by:
Δf=R2πL
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a series LCR circuit, at the frequencies f1 and f2 of AC source, the current amplitude falls to 1√2 of the current amplitude at resonance. Then the value of f2−f1 is
AR2πLBRLCRπLDRπ2LAt resonant frequency the current amplitude in series LCR circuit is
AmaximumBminimumCzeroDinfinityFor the series LCR circuit shown in the figure, what is the resonance frequency and the amplitude of the current at the resonating frequency
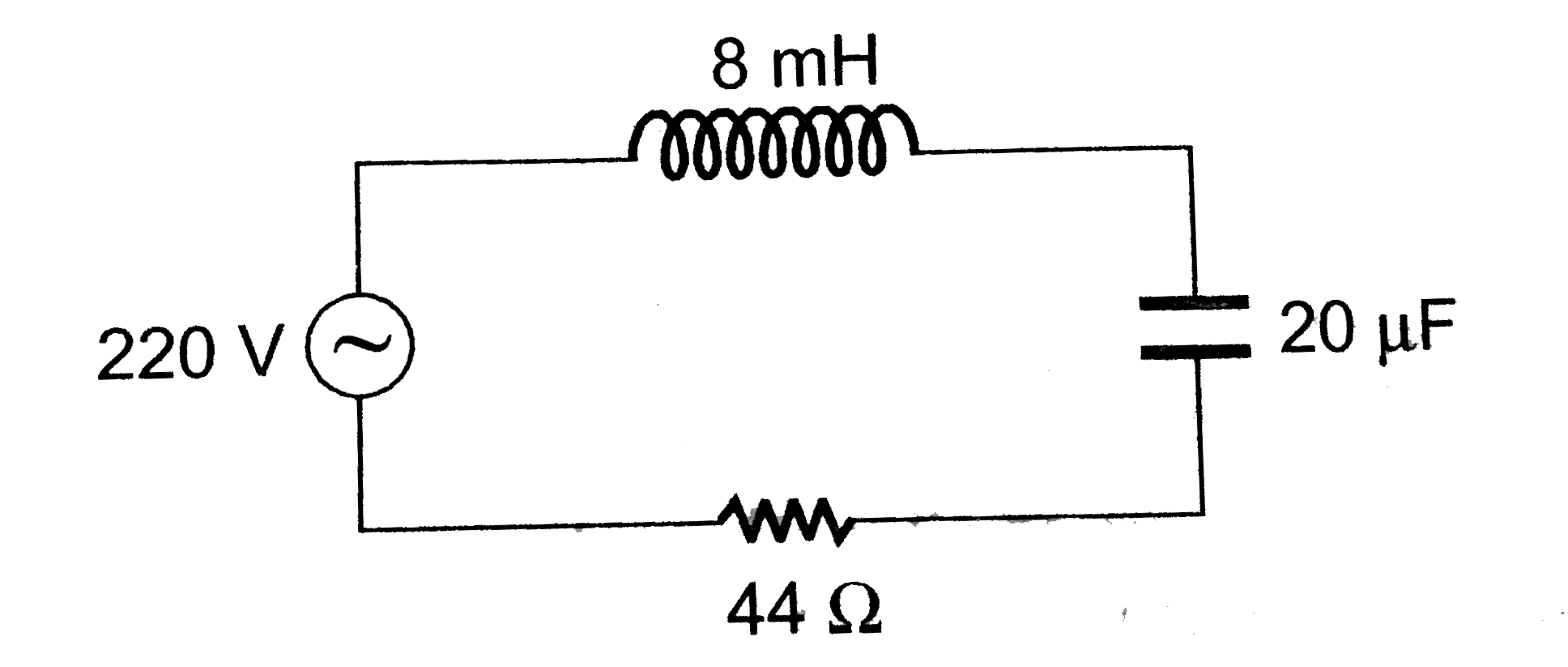 A2500rads−1 and 5√2AB2500rads−1 and 5AC2500rads−1 and 5√2AD25rads−1 and 5√2A
A2500rads−1 and 5√2AB2500rads−1 and 5AC2500rads−1 and 5√2AD25rads−1 and 5√2A
In a series LCR circuit, impedance Z is same at two frequencies f1 and f2. Therefore, the resonant frequency of this circuit is
View SolutionIn the given figure , a series L-C-R circuit is connected to a variable frequency source of 230 V . The impedance and amplitude of the current at the resonating frequency will be
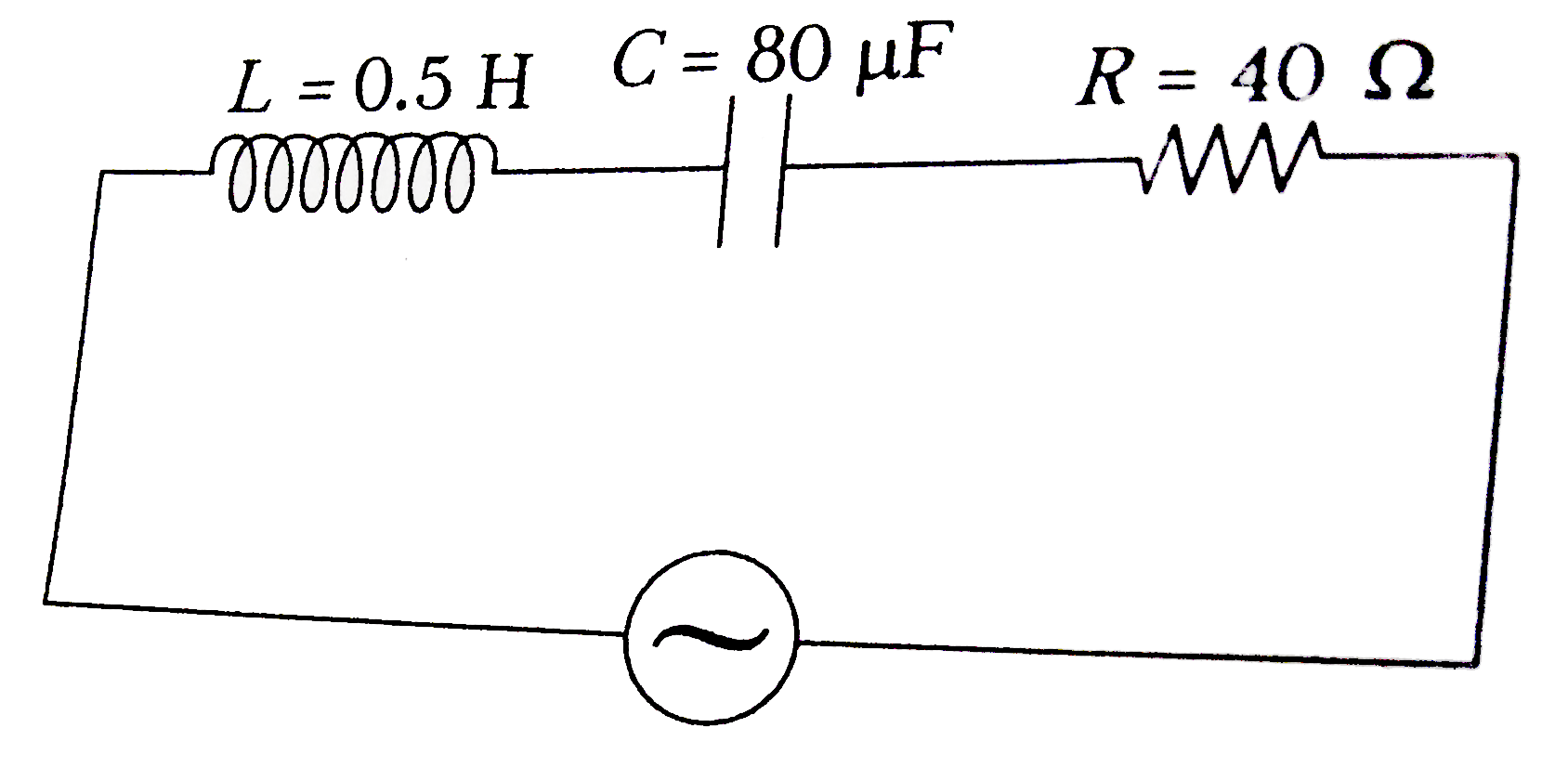
View SolutionWhen L=2H,C=32μF and R=10Ω , then the resonant frequency is:
View SolutionIn R−L−C series circuit, we have same current at angular frequencies ω1 and ω2. The resonant frequency of circuit is
View SolutionFor an RLC circuit driven with voltage of amplitude vm and frequency ω0=1√LC the current exibits resonance. The quality factor, Q is given by :
View Solution
