In a sonometer wire, the tension is maintained by suspending a $50 k g$ mass from the free end of the wire. The suspended mass is completely submerged in water, the fundamental frequency will become …………… $H z$ .

Video Solution

Text Solution

Verified by Experts

$c = v λ$ and $c = \sqrt{T / m}$
$∴ \sqrt{\frac{T}{m}} = v λ$
where $T$ = tension in the string and $m$ = mass per unit length of wire
When $50.7 k g$ mass is suspended for fundamental mode $λ = 2 l$
$v_{1} \times 2 l = \sqrt{\frac{50.7 \times g}{m}}$
when mass in submerged in water, new tension
$T_{2}$ = weight -upthrust
= $50.7 g - 0.0075 \times 1000 \times g = 43.3 g$
$∴ v_{2} \times 2 l = \sqrt{\frac{43.3 g}{m}}$
On dividing Eqs. (i) and (ii), we get
$\frac{v_{2}}{v_{1}} = \sqrt{\frac{43.2}{50.7}} \Rightarrow v_{2} = v_{1} \sqrt{\frac{43.2}{50.7}}$
= $260 \sqrt{\frac{43.2}{50.7}} = 240 H z$ .

Updated on:21/07/2023

In a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m 3. The fundamental frequency of the wire is 260 Hz . If the suspended mass is completely submerged in water, the fundamental frequency will become (take $g = 10 m s^{- 2}$ ) [
A240 Hz
B230 Hz
C220 Hz
D200 Hz
In a sonometer wire the fundamental frequency of the wire is $260 H z$ . In sonometer the tension is maintained by suspending a $50.7 k g$ mass. When the suspended mass is completely submerged in water the fundamental frequency becomes $240 H z$ . The suspended mass has a volume
A $0.002 m^{3}$
B $0.0075 m^{3}$
C $0.004 m^{3}$
D $0.006 m^{3}$
In a sonometer wire, the tension is maintained by suspending a $20 k g$ mass from the free end of the wire. The fundamental frequency of vibration is $300 H z$ .

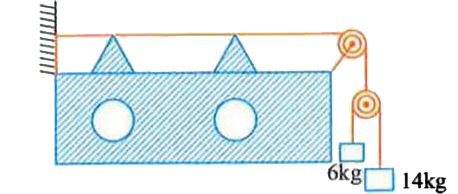
If the tension is provided by two masses of $6 k g$ and $14 k g$ suspended from a pulley as show in the figure the fundamental frequency will
Astill remain $300 H z$
Bbecome larger
Cbecome smaller
Ddecrease in the present situation and increase if the suspended masses of $6 k g$ and $14 k g$ are interchanged