In a sonometer wire, the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has a volume of 0.0075 m 3. The fundamental frequency of the wire is 260 Hz . If the suspended mass is completely submerged in water, the fundamental frequency will become (take $g = 10 m s^{- 2}$ ) [

220 Hz

230 Hz

240 Hz

260 Hz

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

In a sonometer wire, the tension is maintained by suspending a $20 k g$ mass from the free end of the wire. The fundamental frequency of vibration is $300 H z$ .

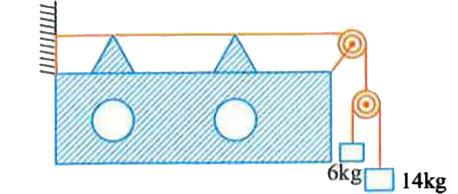
If the tension is provided by two masses of $6 k g$ and $14 k g$ suspended from a pulley as show in the figure the fundamental frequency will
Astill remain $300 H z$
Bbecome larger
Cbecome smaller
Ddecrease in the present situation and increase if the suspended masses of $6 k g$ and $14 k g$ are interchanged
In a sonometer wire the fundamental frequency of the wire is $260 H z$ . In sonometer the tension is maintained by suspending a $50.7 k g$ mass. When the suspended mass is completely submerged in water the fundamental frequency becomes $240 H z$ . The suspended mass has a volume
A $0.002 m^{3}$
B $0.0075 m^{3}$
C $0.004 m^{3}$
D $0.006 m^{3}$
A sonometer wire carries a brass weight of density 8 gm/cc at its free end and has a fundamental frequency 320 Hz, when the brass weight is completely immersed in water , then new frequency will be
A340Hz
B320Hz
C280Hz
D300Hz