In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of hte circle with an angular frequency ω. The axis of rotation is perpendicular to hte field. If the total resistance of hte circuit is R, the mean power generated per period of rotation is
(Bπω)22R
(Bπrω2)22R
Bπr2ω2R
(Bπr2ω)28R
The correct Answer is:D
The magnetic flux linked with the rotating coil is
ϕ=BAcosωt=B⋅(πr22)cosωt
∴ The induced e.m.f. (e) is
∴e=−dϕdt=−B⋅πr22ω(−sinωt)
12Bπr2ωsinωt
∴ Power = e2R=(Bπr2ω)2sin2ωt4R
But the mean value of sin∘ωt=12
∴ Mean power generated per cycle (period) of rotation
=(Bπr2ω)24R×12
Pmean=(Bπr2ω)28R.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS EXERCISE - TEST YOUR GRASP - 16
30 Videos
- ELASTICITYBOOK - MARVEL PUBLICATIONCHAPTER - ELASTICITYEXERCISE - Test Your Grasp - 5
15 Videos
- ELECTRONS AND PHOTONS BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 17
15 Videos
Similar Questions
A wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
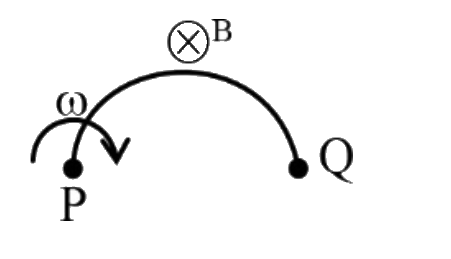
View SolutionA wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
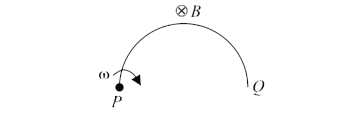
View Solution
Knowledge Check
In a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
A(Bπrω)22RB(Bπr2ω)28RCBπr2ω2RD(Bπrω2)28RIn a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
A(πBr2ω)28RBπBrω28RC(πBrω)28RD0A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View SolutionCalculate the work that has to be done to stop an iron sphere of radius R rotating about its diameter with an angular velocity ω.
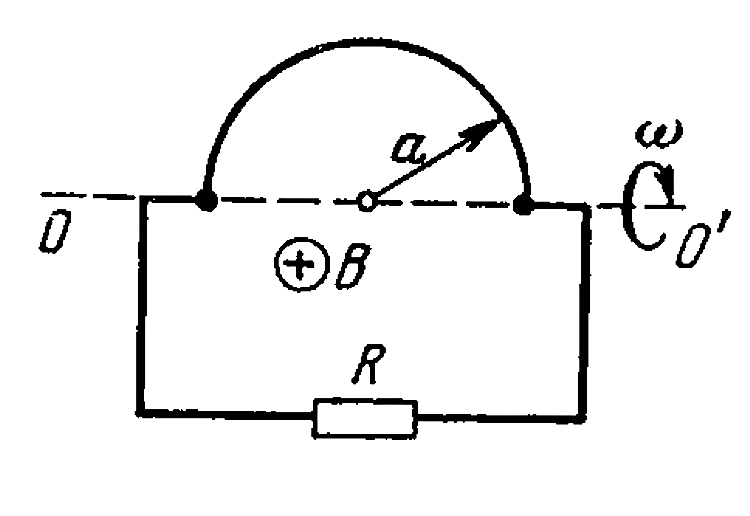
View SolutionA wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionA uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
View Solution
