In above question, speed of block A, when the extension in spring is xm2, is:
2g√mk
2g√2mk
2g√2m3k
g√4m3k
The correct Answer is:D
Topper's Solved these Questions
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 2
18 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 3
34 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Eample
47 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
Consider the situation shown in figure.
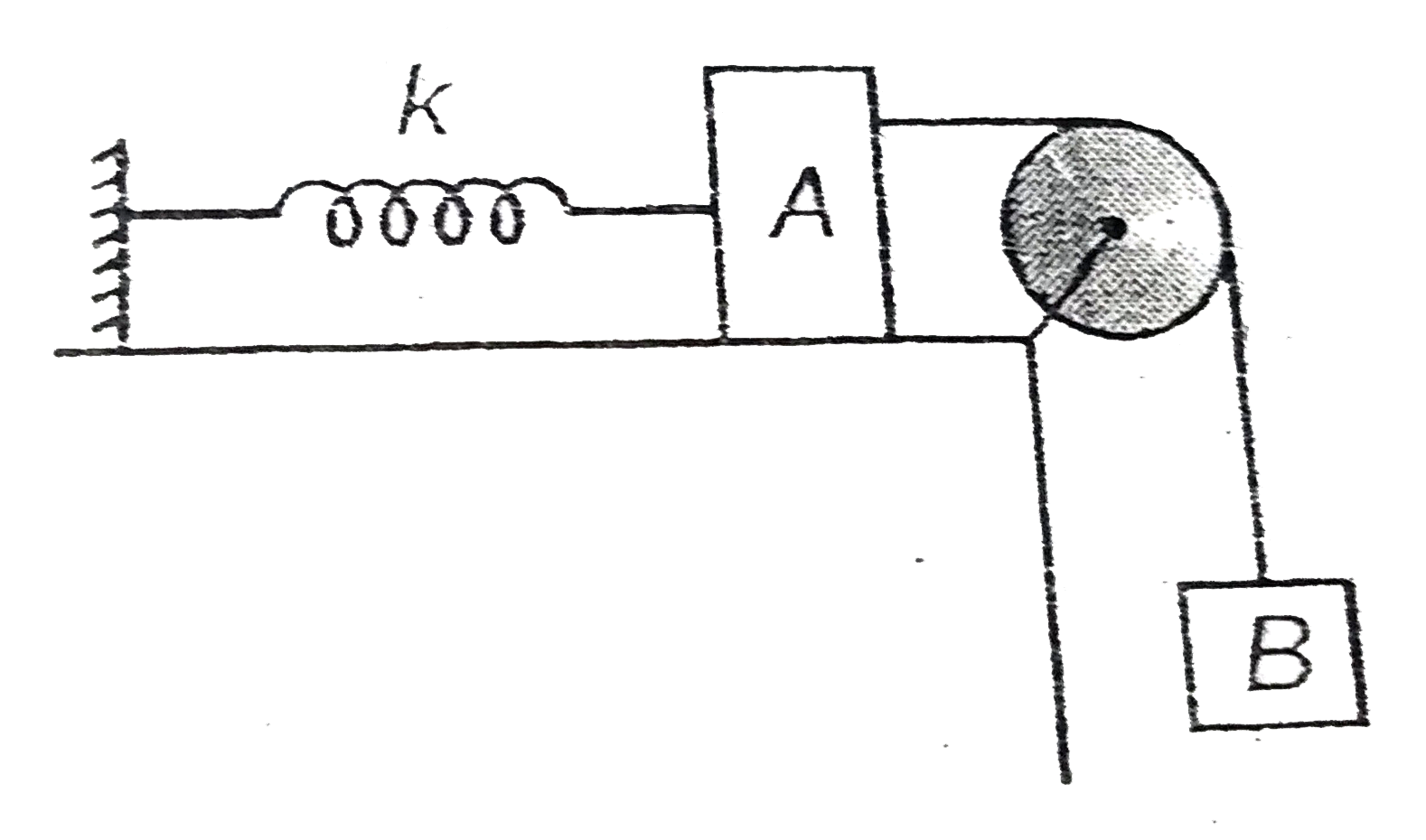
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionConsider the situation shown in figure.

Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View Solution
Knowledge Check
Block A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :
 A2MgK−2x0BMg2K+x0C2MgK−x0D2MgK+x0
A2MgK−2x0BMg2K+x0C2MgK−x0D2MgK+x0Block A in the figure is released from the rest when the extension in the spring is x0. The maximum downward displacement of the block will be :
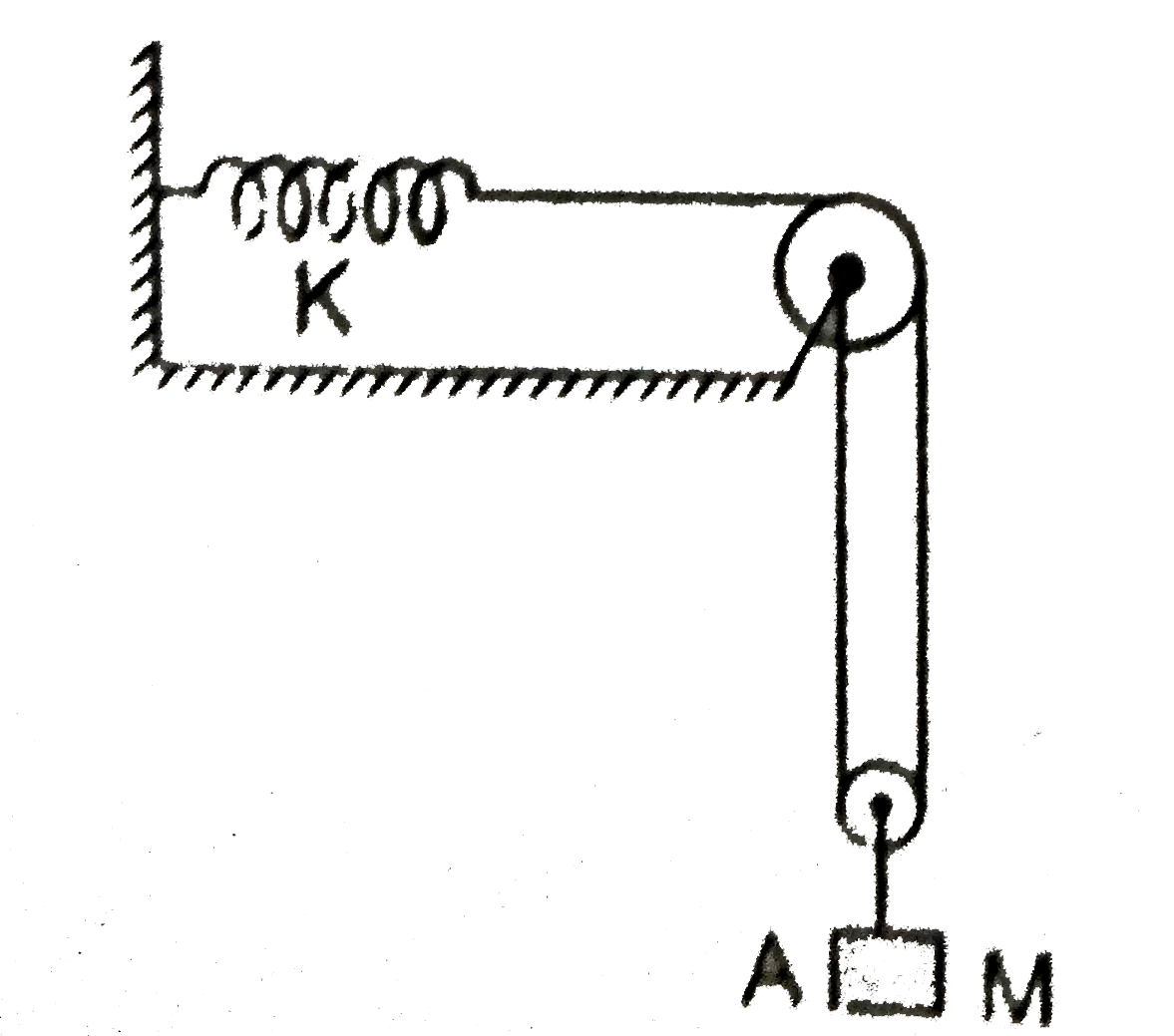 AMg/2k−x0BMg/2k+x0C2Mg/k−x0D2Mg/k+x0
AMg/2k−x0BMg/2k+x0C2Mg/k−x0D2Mg/k+x0Block A of the mass M in the figure is released from rest when the extension in the spring is x0. The maximum downwards displacement of the block is (assume x0<Mg/k).
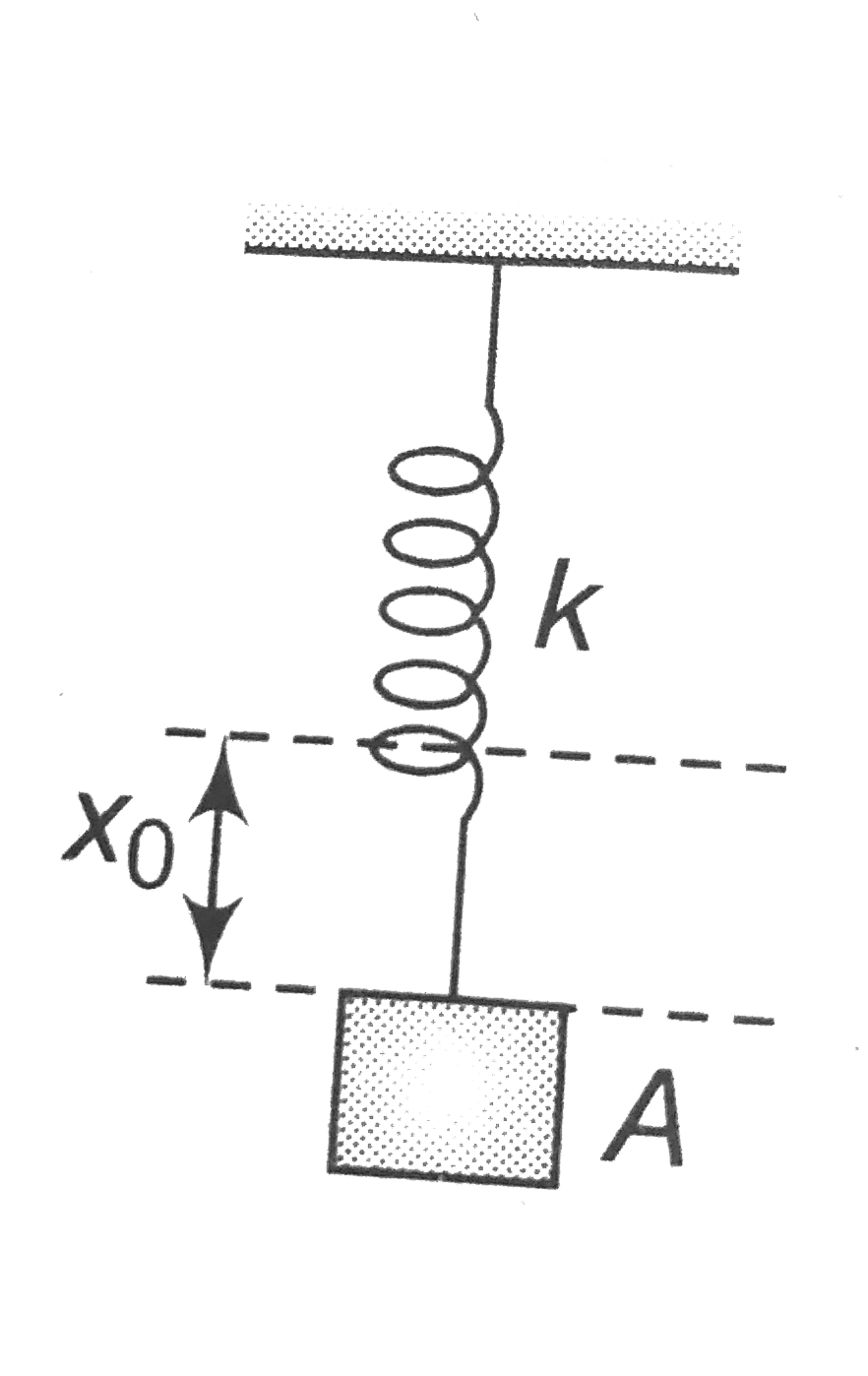 A2(Mgk−x0)BMg2k+x0C2Mgk−x0D2Mgk+x0
A2(Mgk−x0)BMg2k+x0C2Mgk−x0D2Mgk+x0
Block A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :

View SolutionA block of mass 3kg is attached with an ideal spring of spring constant 900 N/m. The other end of the spring connected with a rigid wall. A fixed convex mirror of radius of curvature 120 cm is placed at a distance 110 cm from the block and the spring is in its natural length. the spring is extended by 100 cm and released. the speed of the image of block is (15n)ms, when extension in the spring remains 50 cm. Find the value of 'n'.

View SolutionIf both the blocks moving with constant accelerattion then extension in spring.
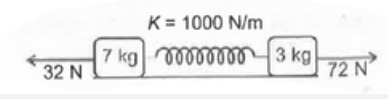
View SolutionIf both the blocks moving with constant accelerattion then extension in spring.

View SolutionIn the above question, the velocity of the rear 2kg block after it separates from the spring will be-
View Solution
