In an electron gun, the potential difference between the filament and plate is 3000 V. What will be the velocity of electron emitting from the gun?
3×108m/s
3.18×107m/s
3.52×107m/s
3.26×107m/s
The correct Answer is:D
To find the velocity of an electron emitted from an electron gun with a potential difference of 3000 V, we can use the principle of energy conservation. The kinetic energy gained by the electron when it is accelerated through the potential difference is equal to the work done on it by the electric field.
1. Understand the relationship between potential difference and kinetic energy:
The work done on the electron by the electric field when it is accelerated through a potential difference V is given by:
W=eV
where e is the charge of the electron (approximately 1.6×10−19 coulombs) and V is the potential difference.
2. Set the work done equal to the kinetic energy:
The kinetic energy (KE) of the electron when it is emitted can be expressed as:
KE=12mv2
where m is the mass of the electron (approximately 9.11×10−31 kg) and v is the velocity of the electron.
3. Equate the two expressions:
Setting the work done equal to the kinetic energy gives us:
eV=12mv2
4. Rearranging the equation to solve for velocity:
Rearranging the equation to solve for v:
v2=2eVm
v=√2eVm
5. Substituting the known values:
Now, substitute e=1.6×10−19 C, V=3000 V, and m=9.11×10−31 kg into the equation:
v=√2×(1.6×10−19)×30009.11×10−31
6. Calculating the value:
First calculate the numerator:
2×(1.6×10−19)×3000=9.6×10−16
Now divide by the mass of the electron:
9.6×10−169.11×10−31≈1.055×1015
Now take the square root:
v≈√1.055×1015≈1.027×107 m/s
Final Answer:
The velocity of the electron emitting from the gun is approximately 1.027×107 m/s.
The work done on the electron by the electric field when it is accelerated through a potential difference V is given by:
W=eV
where e is the charge of the electron (approximately 1.6×10−19 coulombs) and V is the potential difference.
The kinetic energy (KE) of the electron when it is emitted can be expressed as:
KE=12mv2
where m is the mass of the electron (approximately 9.11×10−31 kg) and v is the velocity of the electron.
Setting the work done equal to the kinetic energy gives us:
eV=12mv2
Rearranging the equation to solve for v:
v2=2eVm
v=√2eVm
Now, substitute e=1.6×10−19 C, V=3000 V, and m=9.11×10−31 kg into the equation:
v=√2×(1.6×10−19)×30009.11×10−31
First calculate the numerator:
2×(1.6×10−19)×3000=9.6×10−16
Now divide by the mass of the electron:
9.6×10−169.11×10−31≈1.055×1015
Now take the square root:
v≈√1.055×1015≈1.027×107 m/s
The velocity of the electron emitting from the gun is approximately 1.027×107 m/s.
Topper's Solved these Questions
Similar Questions
Knowledge Check
An electron having charge e and mass m starts from the lower plate of two metallic plates separated by a distance d. If the potential difference between the plates is V, the time taken by the electron to reach the upper plate is given by
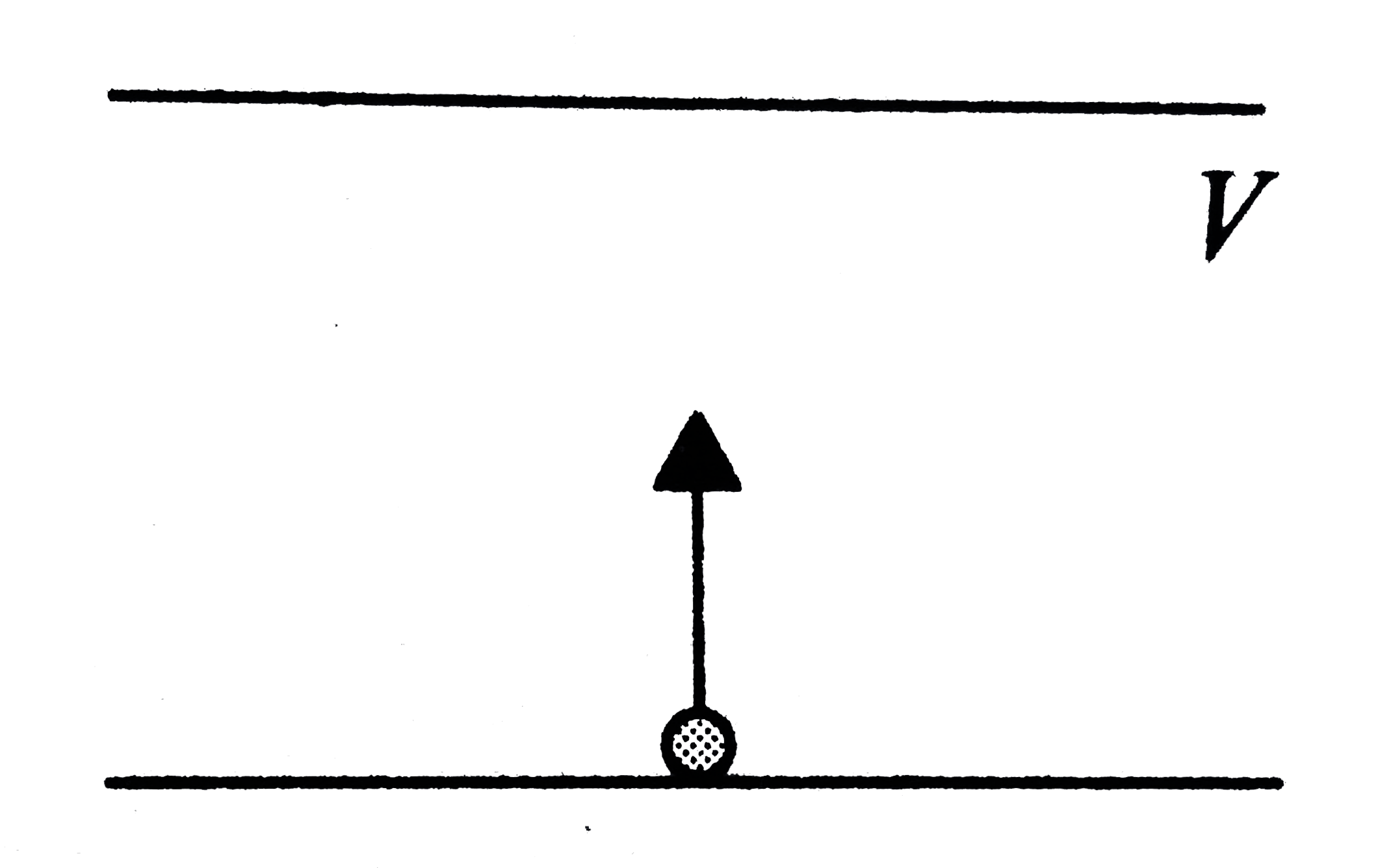 .A√2md2eVB√md2eVC√md22eVD2md2eV
.A√2md2eVB√md2eVC√md22eVD2md2eVAn electron is accelerated from rest to potential V. the final velocity of electron is
A√eV2MB√4eVmC√eVmD√2eVmThe velocity of electrons emitted from the electron gun can be increased by
Aincreasing the filament currentBdecreasing the filament currentCdecreasing the potential difference between the anode and filamentDincreasing the potential difference between the anode and filament
The plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time. After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionThe plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time. After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionAn electron enters the region between the plates of a parallel plate capacitor at a point equidistance from either plate. The capacitor plates are 2×10−2m apart and 10−1m long. A potential difference of 300 V is kept across the plates. Assuming that the initial velocity of the electron is parallel to the capacitor plates, calculate the largest value of the velocity of the electrons so that they do not fly out of the capacitor at the other end.
View SolutionAt the moment t=0 on electron leaves one plate of a parallel-plate capacitor with a neglible velocity. An accelerting volatage, varrying as V=at, where a=100V/s is applied between the plates is l=5.0cm. What is the velocity of the of the electron at the moment it reaches the opposite plate?
View SolutionIn an electron gun the control grid is given a negative potential relative to cathode in order to
View Solution
