In an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
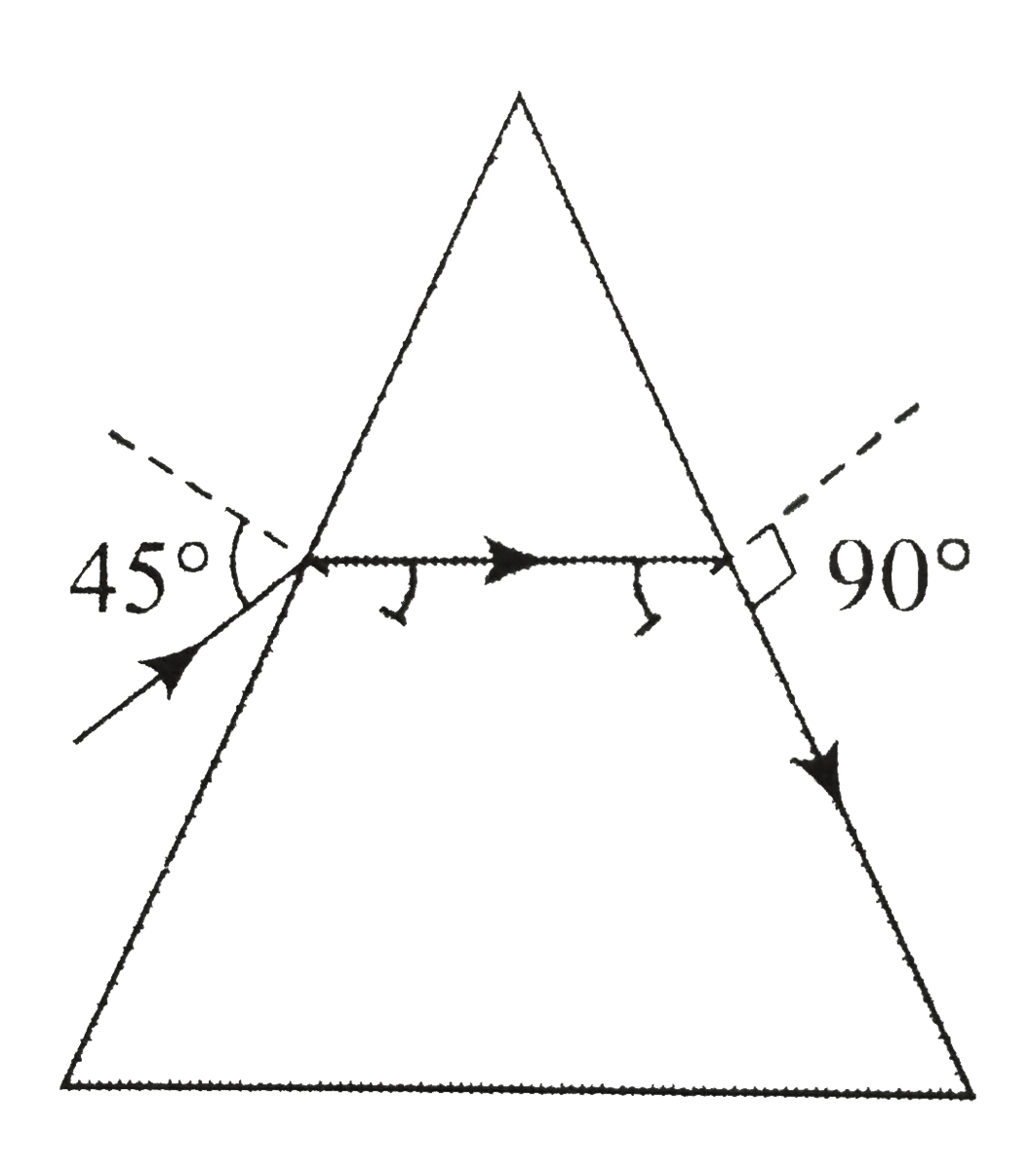
As the ray of light grazes the second surface, r2 is the critical angle.
sinr2=1μ
r2=(45∘−r1)
sinr1=sin45∘μ=1√2μ
sinr2=sin(45∘−r1)
=1√2[cosr1−sinr1]
1μ=1√2[√1−12μ2−1√2μ]
1μ=1√2[√2μ2−1√2μ−1√2μ]
2=√2μ2−1−1
2μ2−1=9
2μ2=10
⇒μ2=5 or μ=√5
At minimum deviation,
r1=r245∘2=22.5∘
μ=sini1sinr1⇒sini1=(√5)sin(22.5∘)
i1=58.8∘
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.5
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.3
25 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
In an isosceles prism of prism angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergent ray grazes the emergent surface. Find the refractive index of the material of the prism.For what angle of incidence the angle of deviation will be minimum ?
View SolutionFor a ray of light refracted through a prism of angle 60∘, the angle of incidence is equal to the angle of emergence, each equal to 45∘. Find the refractive index of the material of the prism.
View Solution
Knowledge Check
The refracting angle of a prism is A and refractive index of the material of prism is cot(A/2) . The angle of minimum deviation will be
A180∘−3AB180∘+3AC90∘−3AD180∘−2AIf the angle of incidence and angle of refraction at the refracting surface are 45∘ and 30∘ respectively, then the refractive index of the material of the prism is
A2B√2C12D1√2A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3
The refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
View SolutionThe refracting angle of a prism is A, and refractive index of the material of the prism is cot(A)2. The angle of minimum deviation is
View SolutionThe refracting angle of a prism is A, the refractive index of the material of the prism is cot(A2). The angle of minimum deviation is :
View SolutionThe refracting angle of a prism is A and refractive index of the material of the prism is cos(A/2). The angle of minimum deviation is
View SolutionA ray of light is incident normally on one of the refracting surfaces of a prism of refracting angle A,. The emergent ray grazes the other refracting surface. Find the refractive index of the material ofprism.
View Solution
