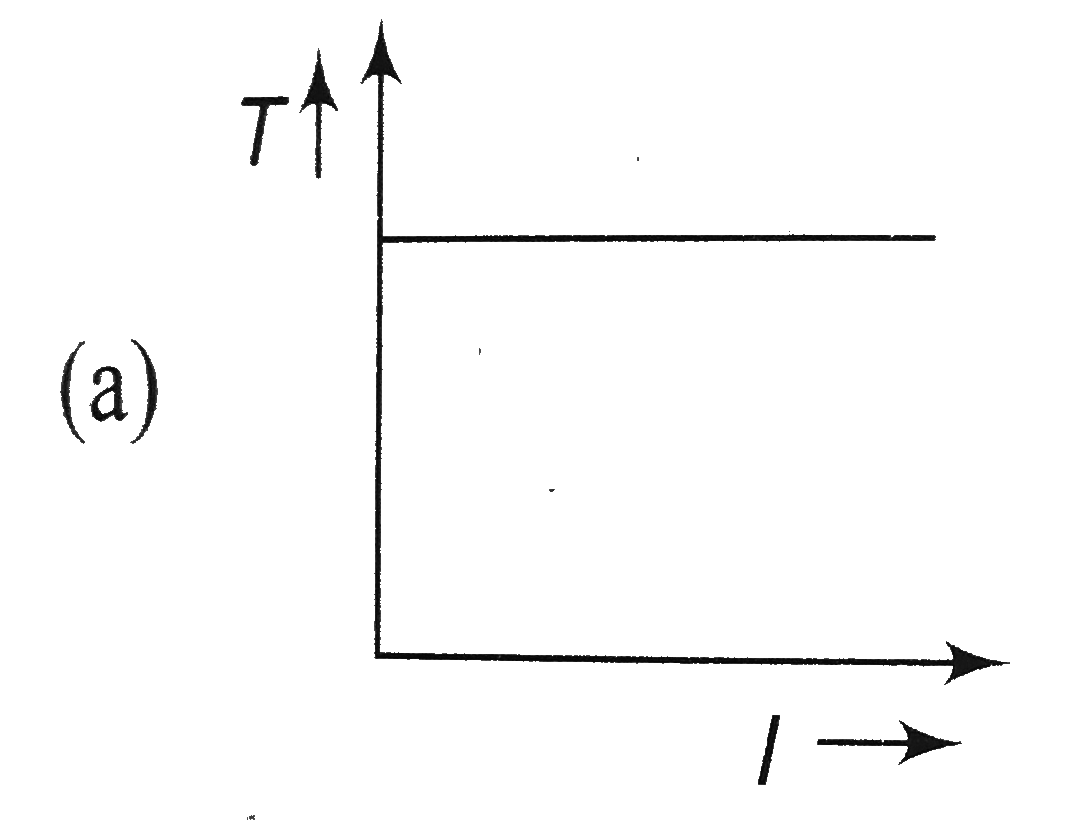
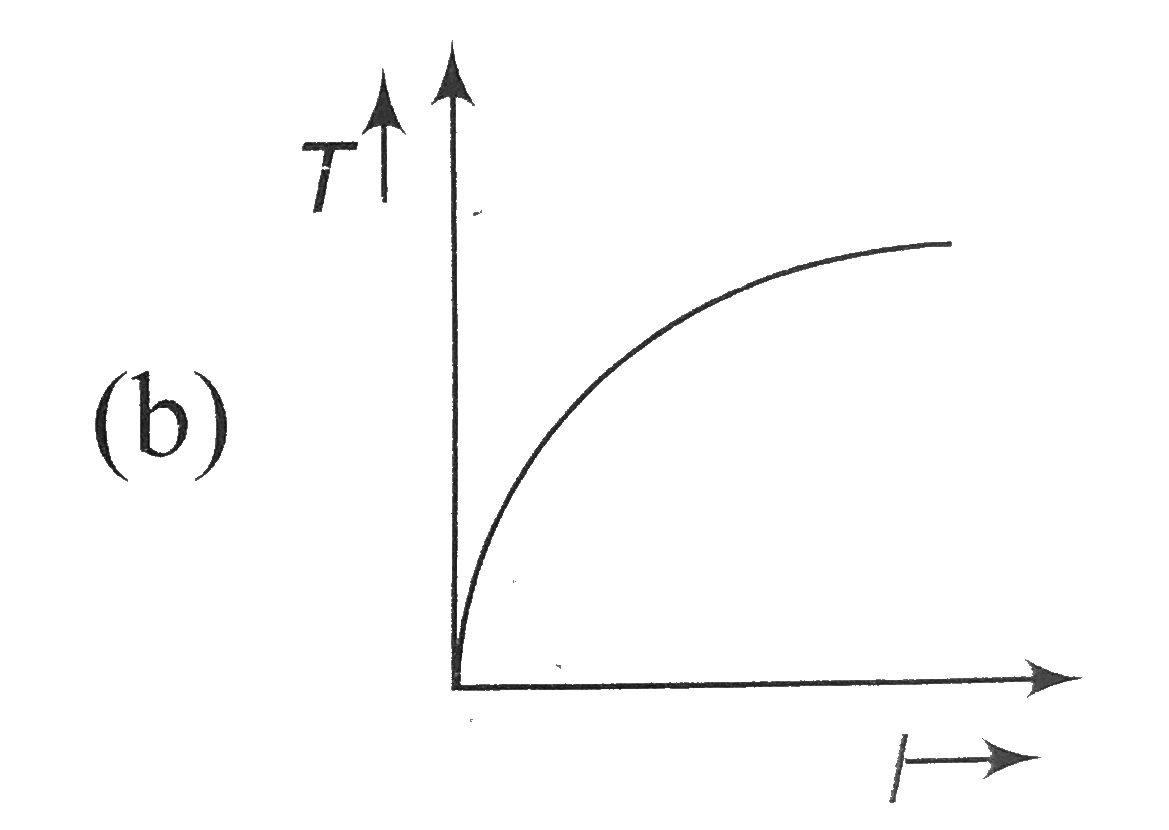
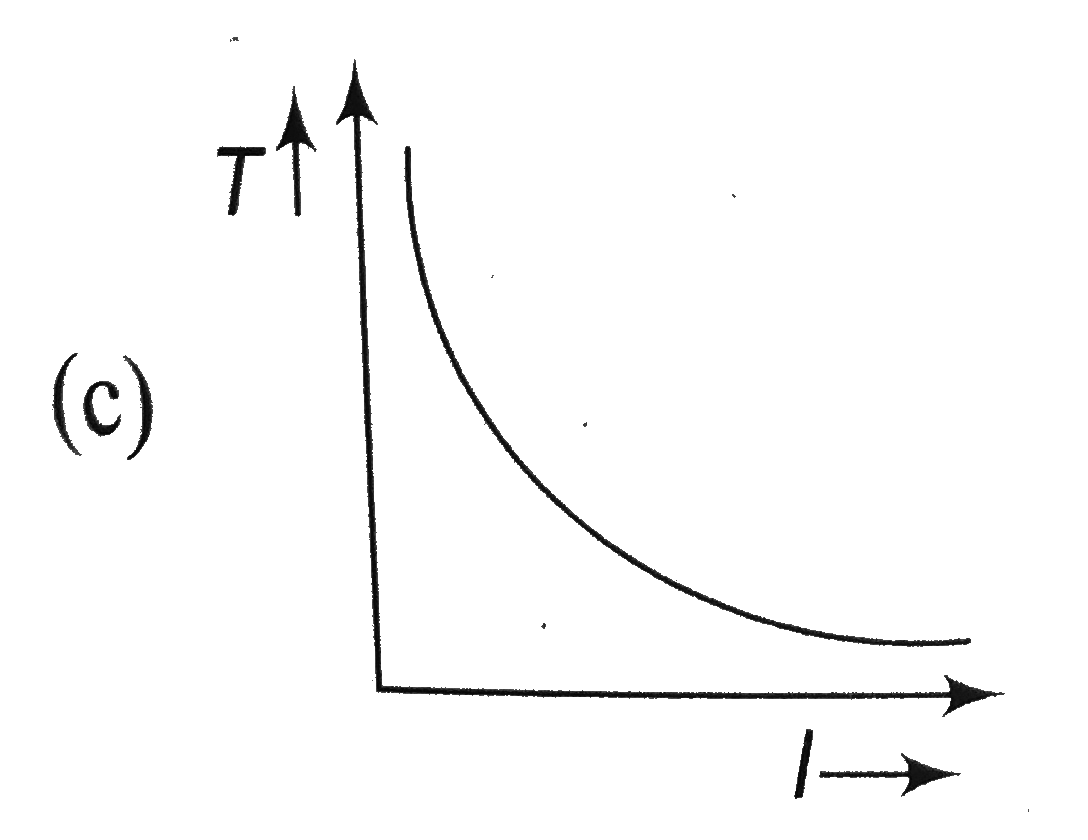
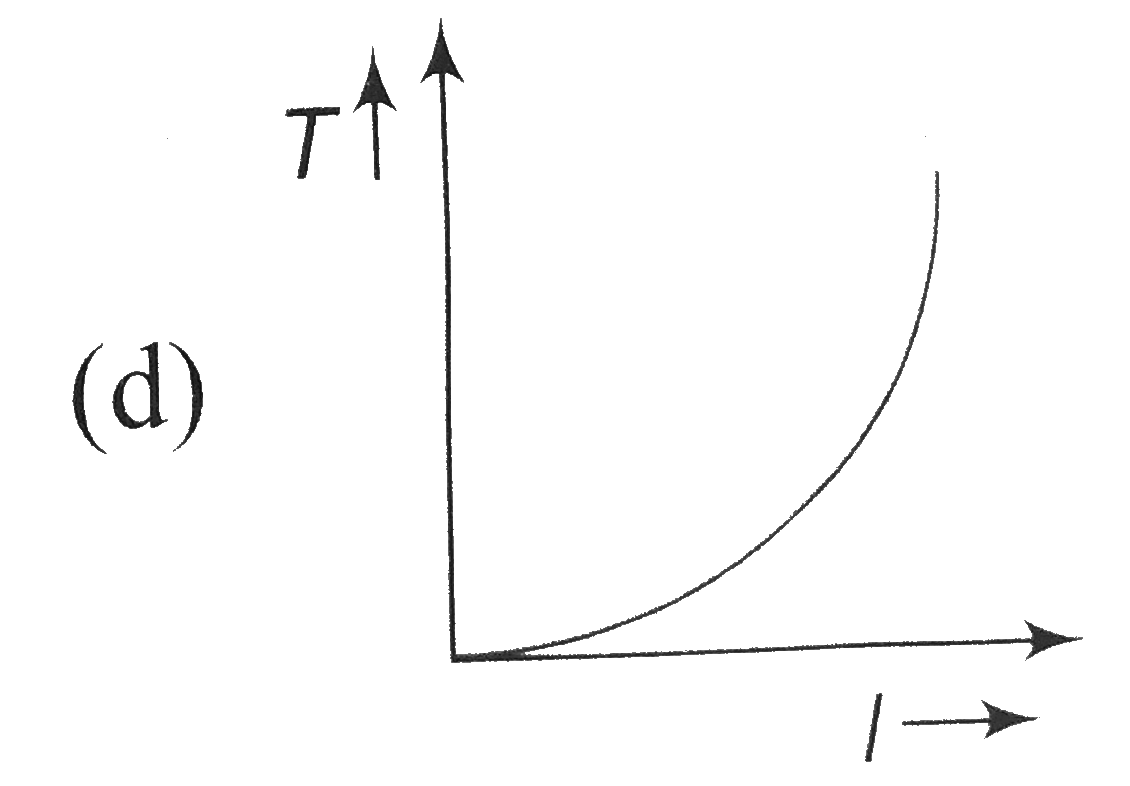
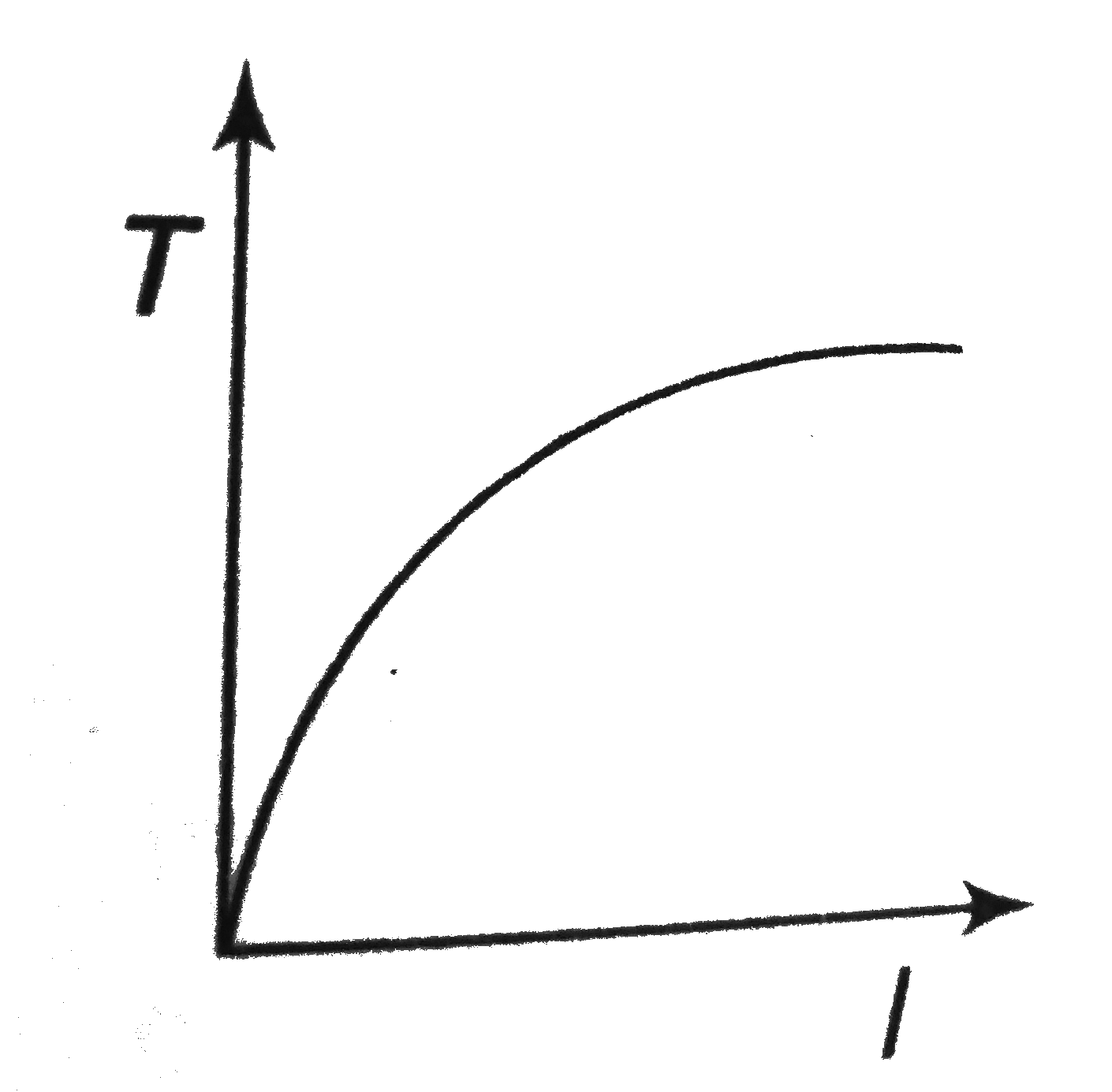
In case of a simple pendulum, time period versus length is depicted by
A
B
C
D
Video Solution
Text Solution
The correct Answer is:B
T=√1⇒T2∝1
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum19videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Problems Based On Mixed Concepts24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
Time period of simple pendulum is
AT=2π√lgBT=2π√glCT=√2πlgDT=12π√gl - Question 2 - Select One
An amplitue of a simple pendulum of a period 'T' and length 'L' is increased by 5%. The new period of that pendulum will be
AT8BT4CT2DT - Question 3 - Select One
The period of a simple pendulum is double, when its length is increased by 1.2 m. The original length of the simple pendulum is
A0.2 mB0.3 mC0.4 mD0.5 m
The time period of a simple pendulum is 2s. It its length is increased by 4 times, then its period becomes
View SolutionThe time period of a simple pendulum of infinte length is
View SolutionIn the case of a simple pendulum, a graph is drawn between the displacement and time taken for its oscillations as shown in the figure. Then
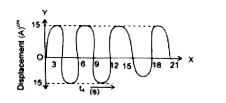
Time period of the pendulum bob is ______ s.View SolutionThe time period of oscillation of a simple pendulum is √2s. If its length is decreased to half of initial length, then its new period is
View SolutionThe time period of simple pendulum is T. If its length is increased by 2%, the new time period becomes
View Solution

