In fig. 16-47a, string 1 has a linear density of 3.00 g/m, and string 2 has a linear density of 5.00 g/m. They are under tension due to the hanging block of mass M= 800 g. Calculate the wave speed on (a) string 1 and (b) string 2 (Hint: When a string loops halfway around a pulley, it pulls on the pulley witii a net force that is twice the tension in the string) Next the block is divided into two blocks (with M1+M2=M) and the apparatus in tearranged as shown in fig. 16-47b. Find (c) M1and(d)M2 such that the wave speeds in the two strings are equal.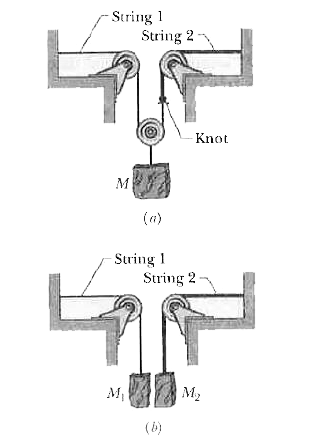 
The correct Answer is:(a) 36.2m/s; (b) 28.0m/s; (c) 300g (d) 500g
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Single Correct Choice Type)33videos
WAVES-I
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (More than One Coorect Choice Type)10videos
WAVES-I
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Checkpoint8videos
WAVES-I
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)5videos
WAVE - II
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Integer Type)5videos
WORK, POWER, AND ENERGY
Similar Questions
Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
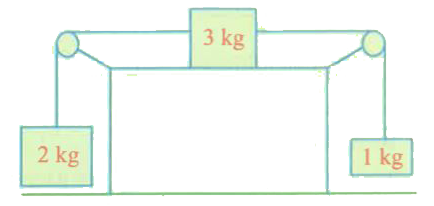
View SolutionThe system as shown in fig is released from rest. Calculate the tension in the strings and force exerted by the strings on the pulley. Assuming pulleys and strings are massless
View Solution
Knowledge Check
- Question 1 - Select One
A string of length 0.5m and linear density 10−4 kg/m is stretched under a tension of 100 N. If the frequency of the vibration of the string is 4000 Hz, how many loops are formed on the string?
A1B4C2D6 - Question 2 - Select One
The tension in a string with a linear density of 0.0010 kg/m iş 0.40 N. A 100 Hz sinusoidal wave on this string has a wavelength of
A0.05cmB2.0cmC5.0cmD20cm - Question 3 - Select One
Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2g
The system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.
View SolutionThe system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.
View SolutionThe linear density of a string is 1.9×10−4kg/m. A transverse wave on the string is described by the equation
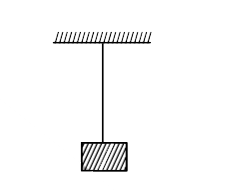
y=(0.021m)sin[(2.0m−1)x+(30s−1)t]. What are (a) the wave speed and (b) the tension in the string?View SolutionA 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)
View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :
View Solution