In L−C−R series AC circuit,
If R is increased, then current will decrease
If L is increased, then current will decrease
If C is increased, then current will increase
If C is increased, then current will decrease
The correct Answer is:A
I=VZ
=V√R2+(ωL~1ωC)2
By increasing R current will definitely decrease by change in L or C, current may increase or decrease.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Comprehension6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Subjective10videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2 Single Correct18videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
In an L-C-R series, AC circuit at resonance
View SolutionAssertion: In L-C-R series AC circut, XL=XC=R at a given frequency. When frequency is doubled, the impedance of the circuit is √132 R.
Reason: The given frequency is resonance frequency.View SolutionMatch the following two columns for L-C-R series AC circuit.
 View Solution
View SolutionIn L−C−R series circuit
View SolutionIn an L-C-R series circuit R = 10Ω,XL=8Ωand XC=6Ωthe total impedance of the circuit is -
View SolutionAn L-C-R series circuit , connected to a source E, is at resonance. Then,
View SolutionIn an LCR series ac circuit , the voltage across each of the components , L,C and R is 50 V . The voltage across the LC combination will be :
View SolutionIn an L-C -R series circuit connected to an AC source V=V0sin(100π(t)+π6)VR=40V,VL=40andVC=10V, resistance R=4Ω
peak value of current isView SolutionWhich increase in frequency of an AC supply , the impedance of an L-C-R series circuit
View SolutionIn an AC, series L-C-R circuit, R=XL=XC and applied AC, voltage is V. Then match the following two columns.
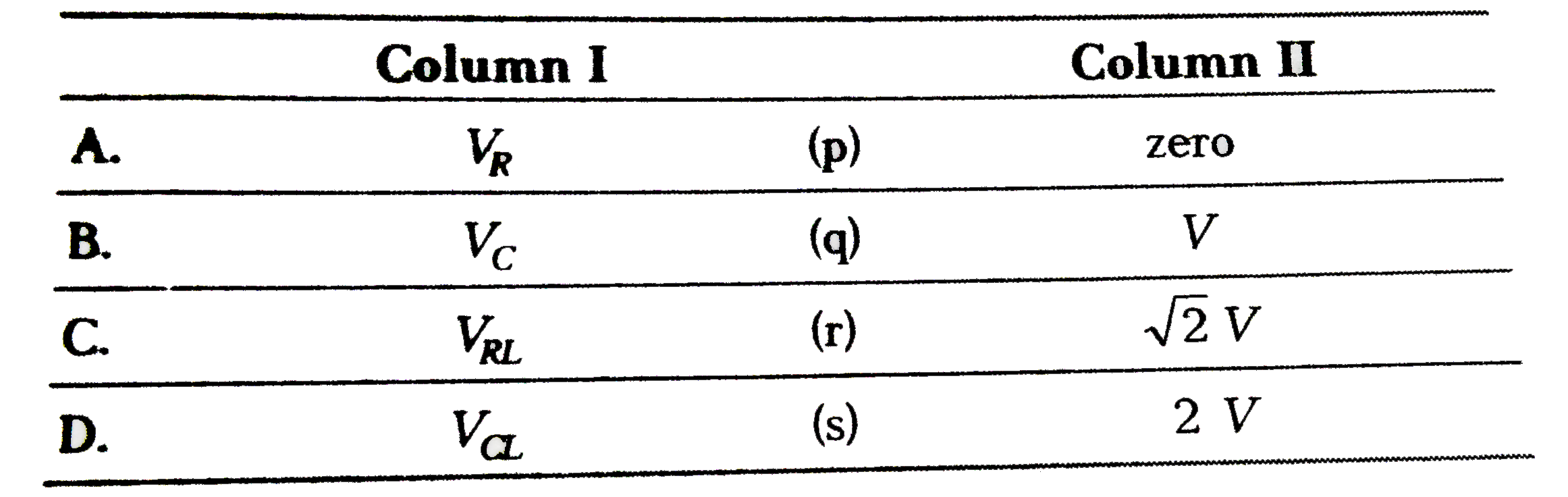 View Solution
View Solution
