In many experimental set-ups, the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these pionts and the ratio of the image sizes for these two points. Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

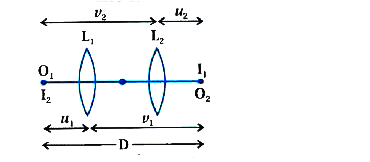
$\Rightarrow$ According to law of reversibility of light , ray, we con interchange the positions of object and its image for a given convex lens. Now, according image for a given convex lens. Now , according to lens formula,
$\frac{1}{f} = \frac{1}{v} - \frac{1}{u} ... ... (1)$
Now,according to sign convetion in above figure,
$∴ - u + v = D ... ... (2)$
$∴ u = - (D - v)$
Placing above vlaue in equation (1),
$\frac{1}{f} = \frac{1}{v} + \frac{1}{D - v}$
$∴ \frac{1}{f} = \frac{D}{v (D - v)}$
$∴ \frac{1}{f} = \frac{(D - v) + v}{v (D - v)}$
$∴ D v - v^{2} = D f$
$∴ D v - v^{2} = D f$
$∴ v^{2} - D v + D f = 0$ ........(3)
$∴ v = (D \pm \frac{\sqrt{D^{2} - 4 D f}}{2})$
$\Rightarrow$ Above is quadratic equaiton in terms of v whose two roots are,
$v = \frac{- (- D) \pm \sqrt{{(- D)}^{2} - 4 (1) (D f)}}{2 (1)}$
$∴ v = \frac{D \pm \sqrt{D^{2} - 4 D f}}{2}$ .....(4)
$\Rightarrow$ From equation (2) and (4)
$\Rightarrow$ From equation (2) and (4)
$u = - (D - \frac{D \pm \sqrt{D^{2} - 4 D f}}{2})$
$= - (\frac{2 D - D \pm \sqrt{D^{2} - 4 D f}}{2})$
$∴ u = - (\frac{D}{2} \pm \frac{\sqrt{D^{2} - 4 D f}}{2})$ ......(5)
$\Rightarrow$ From equations (4) and (5), we can say that
$(i) if u_{1} = \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2}$ then
$v_{1} = \frac{D}{2} + \frac{\sqrt{(D^{2} - 4 D f)}}{2}$
(ii) if $u_{2} = \frac{D}{2} - \frac{\sqrt{D^{2} - 4 D f}}{2}$ then
$v_{2} = \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2}$
$\Rightarrow$ Now, for above two object distances, if distance between corresponding tow positions of lens is d then ,
$d = \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2} - (\frac{D}{2} - \frac{\sqrt{D^{2} - 4 D f}}{2})$
$d = \sqrt{D^{2} - 4 D f}$
If $μ_{1} = \frac{D}{2} + \frac{d}{2}$ then image distance is $v_{1} = \frac{D}{2} - \frac{d}{2}$
and magnification $m_{1} = \frac{v_{1}}{u_{1}} = \frac{\frac{D}{2} - \frac{d}{2}}{\frac{D}{2} + \frac{d}{2}} = \frac{D - d}{D + d}$
Now if $u_{2} = \frac{D}{2} - \frac{d}{2}$ then $v_{2} = \frac{D}{2} + \frac{d}{2}$
and magnification $m_{2} = \frac{v_{2}}{u_{2}} = \frac{D + d}{D - d}$
$∴$ Ration $\frac{m_{2}}{m_{1}} = {(\frac{D + d}{D - d})}^{2}$
$\Rightarrow$ Note : Here for real roots of equation (3),
$D^{2} - 4 D g > 0$
$∴ D^{2} > 4 D f$
$∴ D > 4 f$
$t h e r e r f or e D_{min} = 4 f$
$\Rightarrow$ Minimum distance between object and its real image obtained by convex lens should be 4f (where f = focal length of that convex lens ).

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-RAY OPTICS AND OPTICAL INSTRUMENTS-SECTION-C (NCERT EXEMPLAR SOLUTION) (SHORT ANSWER TYPE QUESITONS)

Home
Ask Doubt
Profile