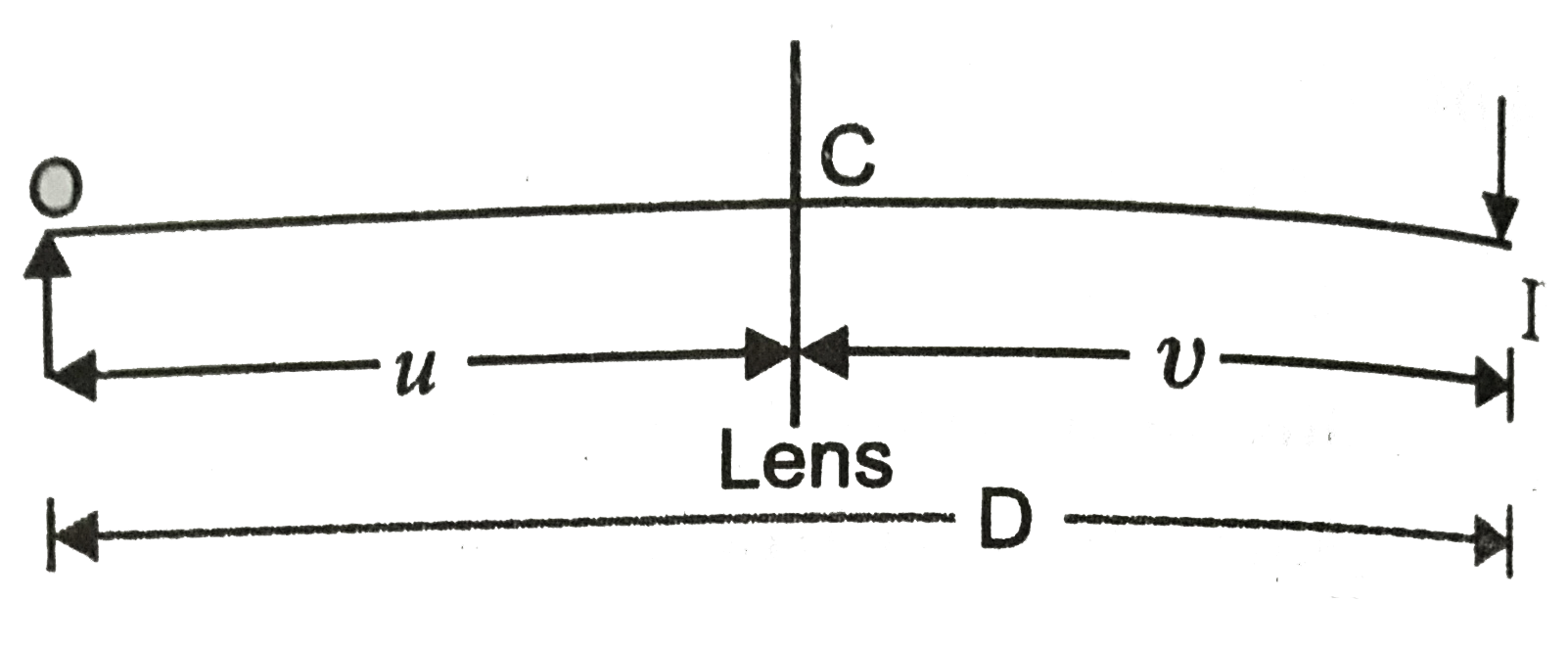
In may experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.
In the lens formula, 1f=1v−1u
we find that u and v are reversible. Therefore, there are two positions of the object, for which there will be an image on the screen.
Let the first position be when lens is at C, Fig.
∴−u+v=D = distance between source (O) and screen I.
or u=−(D−v)
Put in (i)
1v+1D−v=1f or D−v+vv(D−v)=1f or Dv−v2=Df or v2−Dv+Df=0
∴v=D±√D2−4Df2=D2±√D2−4Df2
and u=−(D−v)=−[D2±√D2−4Df2].
Thus if object distance is u=D2+√D2−4Df2, then image distance is v=D2−√D2−4Df2
Again, if object distance is u=D2−√D2−4Df2 then image distance is v=D2+√D2−4Df2
The distance between two positions of the lens for these two object distance is
d=D2+√D2−4Df2−D2+√D2−4Df2=√D2−4Df
If u=D2+d2, then v=D2−d2∴ Magification, m1=vu=D−dD+d
If u=D2−d2, then v=D2+d2∴ Magnification, m2=vu=D+dD−d.
 .
.
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Long Answer (b)
15 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Long Answer (c)
8 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Short Answer(d)
17 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
A thin converging lens is placed between an object and a screen whose position are fixed. There are two positions of the lens at which the sharp image of the object is formed on the screen. Find the transverse dimension of the object if at one position of the lens the image dimension equal h'=2.0mm and at the other, h''=4.5mm.
View SolutionFinding focal length by displacement method
In an experiment for finding focal length of a convex lens the object and screen are kept fixed. There are two position of lens between the object and screen for which an image is obtained on the screen. These positions are separated by 20cm. Also, the magnification in first situation is -2. Find the distance between the object and the screen, that is the focal length of the lens.
View Solution
Knowledge Check
An object and a screen are kept at a distance of 120 cm A lens of focal length 22.5 cm is kept between them so that a real image is formed on the screen Find the possible location (s) of the lens.
A90cm from objectB30cm from objectC40cm from objectD80cm from objectA thin convergent lens is placed between an object and a screen whose positions are fixed. There are two positions of a lens at which sharp image of the object is formed on the screen. If the size of the images in the two cases are 2 mm and 4.5 mm then the size of the object should be:-
A1mmB2mmC3mmD4mmThe magnifications for two positions of image of the same lens are 3 and 2, of a fix point object on a fix screen when the distance between the two positions of lens is 30 cm .
The focal lengths of the lens isA180 cmB90 cmC30 cmD15 cm
An object and a screen are placed 80 cm apart. There are two positions at which a convex lens forms a real image on the screen, the magnification in the cases being 3/2 and 2/3. Calculate the focal length of the lens.
View SolutionA convex lens is placed between an object and a screen which are at a fixed distance apart for one position of the lens. The magnification of the image obtained on the screen is m1. When the lens is moved by a distance d the magnification of the image obtained on the same screen m2, Find the focal length of the lens.
View SolutionA source of light and screen are separated by a distance of 50 cm. A sharp image of the source is produced by lens when placed at two positions between the source and the screen. If the distance of separations of the lens between the two positions is 20 cm, find the focal length of the lens.
View SolutionA convex lens forms a real image on a screen placed at a distance 60 cm from the object. When the lens is shifted towards the screen by 20 cm , another image of the object is formed on the screen. The focal length of the lens is :
View SolutionThe distance between the object and the screen is d (greater than 4 times the focal length of a convex lens). Real images of the object are obtained on the screen for two positions of the lens that are separated by distance x apart. The ratio of size of the images in the two positions of the lens are
View Solution
