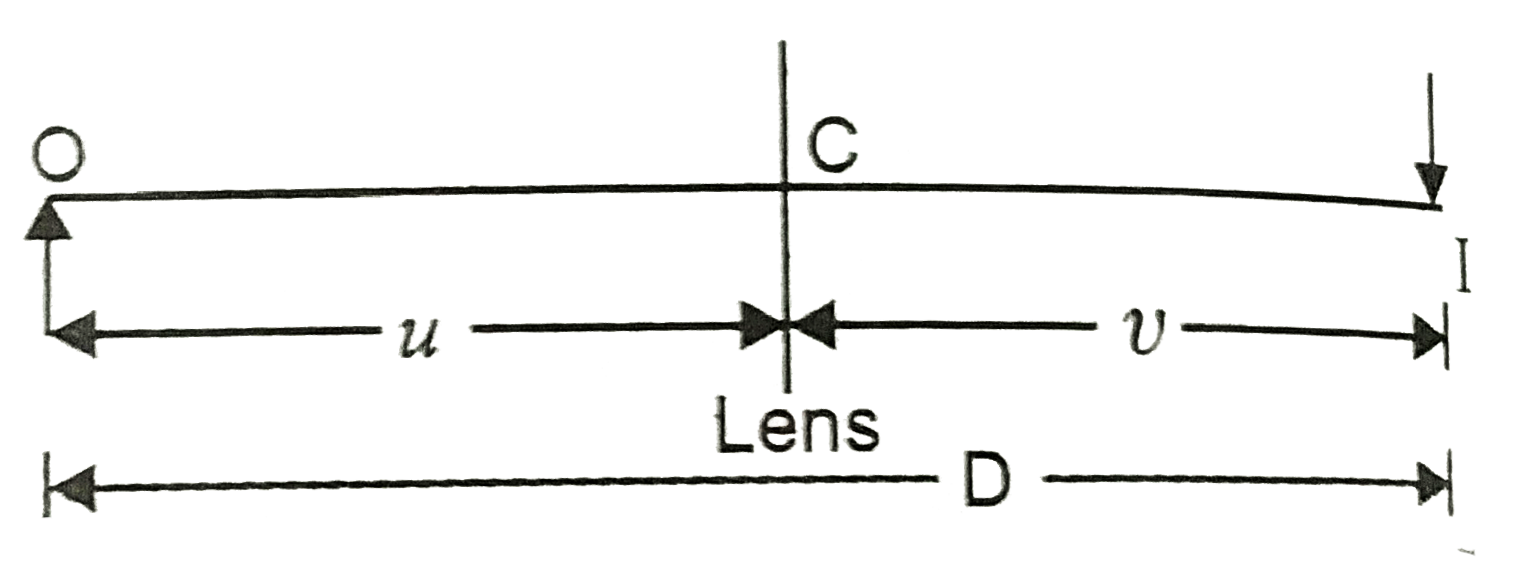
In may experimental set-ups the source and screen are fixed at a distance say $D$ and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.

Video Solution

Text Solution

Verified by Experts

In the lens formula, $\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$
We find that u and v reversible. Therefore, there are two positions of the object, for which there will an image on the screen.
Let the first position be when lens is at $C$ , Fig.
$∴ - u + v = D =$ distance between source (O) and screen I.
or $u = - (D - v)$
Put in (i)
$\frac{1}{v} + \frac{1}{D - v} = \frac{1}{f} or \frac{D - v + v}{v (D - v)} = \frac{1}{f} or D v - v^{2} = D f or v^{2} - D v + D f = 0$ .
$∴ v = \frac{D \pm \sqrt{D^{2} - 4 D f}}{2} = \frac{D}{2} \pm \frac{\sqrt{D^{2} - 4 D f}}{2} and u = - (D - v) = [\frac{D}{2} \pm \frac{\sqrt{D^{2} - 4 D f}}{2}]$
Thus if object distance is $u = \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2}$ , then image distance is $v = \frac{D}{2} - \frac{D}{2} - \frac{\sqrt{D^{2} - 4 D f}}{2}$
Again, if object distance is $u = \frac{D}{2} - \frac{\sqrt{D^{2} - 4 D f}}{2}$ , then image distance is $v = \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2}$
The distance between two position of the lens for these two object distance is
$d = \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2} - \frac{D}{2} + \frac{\sqrt{D^{2} - 4 D f}}{2} = \sqrt{)} (D^{2} - 4 D f)$
If $u = \frac{D}{2} + \frac{d}{2}$ , then $v = \frac{D}{2} - \frac{d}{2} ∴$ magnification, $m_{1} = \frac{v}{u} = \frac{D - d}{D + d}$
If $u = \frac{D}{2} - \frac{d}{2}$ , then $v = \frac{D}{2} + \frac{d}{2} ∴$ magnification, $m_{2} = \frac{v}{u} = \frac{D + d}{D - d}$ .

An object and a screen are kept at a distance of 120 cm A lens of focal length $22.5$ cm is kept between them so that a real image is formed on the screen Find the possible location (s) of the lens.
A90cm from object
B30cm from object
C40cm from object
D80cm from object
A thin convergent lens is placed between an object and a screen whose positions are fixed. There are two positions of a lens at which sharp image of the object is formed on the screen. If the size of the images in the two cases are 2 mm and 4.5 mm then the size of the object should be:-
A1mm
B2mm
C3mm
D4mm
The magnifications for two positions of image of the same lens are 3 and 2, of a fix point object on a fix screen when the distance between the two positions of lens is 30 cm .
The focal lengths of the lens is
A180 cm
B90 cm
C30 cm
D15 cm