In nature the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus, the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by is the Young's modulus, r is the radius 4R of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.Solution in Gujrati
Let us see the diagram of the given situation according to the problem the bending torque on the trunk of radius r of tree
where R is the radius of curvature of the bent surface,
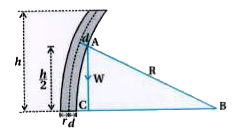
when trunk is bend then,
then the centre of gravity of tree is at a height from the ground.
From
If then
Torque is caused by the weight]
Hence, critical height
Topper's Solved these Questions
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-E
28 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-F
11 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-C
66 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D
1 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - QUESTION PAPER (SECTION -C)
3 Videos
Similar Questions
Two wires A and B are of the same material their lengths are in the ratio 1 : 2 and the diameter are in the ratio 2 : 1. If they are pulled by the same force, their increase in length will be in the ratio ........
View SolutionTwo wires are made of the same material and have the same volume. The first wire has cross sectional area A and the second wire has cross sectional area 3A. If the length of the first wire is increased by Δl on applying a force F, how much force needed to stretch the second wire by the same amount ?
View SolutionWhat is elasticity ? What is plastic body and plasticity?
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm . If the amount of glycerine collected per second at one is 4.0×10−3kgs−1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine =1.3×10103kgm−3 and viscosity of glycerine =0.83 Pa s). [ you may also like to check if the assumption of laminar flow in the tube is correct]
View SolutionIn nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus, the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by Yπr44R. Y is the Young's modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
View SolutionStatement-1 : Earthquakes cause vast devastation. Sometimes short and tall structures remain unaffected while the medium height structures fall
Statement-2 : The natural frequency of the medium structures coincides with the frequency of the seismic wave.
View SolutionIn nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus, the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by Yπr44R. Y is the Young's modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
View SolutionDoes a bar magnet exert a torque on itself due to its own field?
View SolutionWhat is meant by torque due to gravity?
View Solutionஓர் பெரிய அமைப்பினை அல்லது பொருளை அதனுள் அபங்கிய நுண்ணிய துகள்களின் மூலம் விளக்க முயற்சிப்பதே ___________
View SolutionIn nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus, the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by Yπr44R. Y is the Young's modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
View SolutionHow much is the torque due to gravity on a body about its centre of mass ?
View Solutionप्रकृति में, प्रायः संरचनात्मक अवयवों के क्षय का कारण तनन अथवा संपीडन विकृतियों के बजाय ऐंठन अथवा बंकन के कारण उत्पन्न विशाल बल आपूर्ण होते हैं। संरचनाओं के इस प्रकार भंग होने की प्रक्रिया को आकुंचन कहते हैं तथा वृक्षों जैसी विशाल बेलनाकार संरचनाओं के प्रकरणों में यह बल-आघूर्ण अपने स्वयं के भार के कारण उत्पन्न होकर संरचना को बंकित कर देता है। अत: गुरुत्व केंद्र से गुजरने वाली ऊर्ध्वाधर रेखा संरचना के आधार से नहीं गुजरती। इस बंकन के कारण वृक्ष की केंद्रीय अक्ष के परितः प्रत्यास्थ चल आघूर्ण Yπr44R द्वारा व्यक्त किया जाता है, यहाँ Y यंग गुणांक, r तने की शिया तथा वृक्ष की लंबाई के अनुदिश गुरुत्व केंद्र युक्त बंकित पृष्ठ (उदासीन पृष्ठ की वक्रता त्रिज्या है)। वृक्ष के तने की किसी दी गयी त्रिज्या के लिए वृक्ष की क्रांतिक ऊँचाई का आकलन कौजिए।
View SolutionIn nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structureslike trees, the torque is caused by its own weight bending the structure. Thus the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by Yπr44R. Y is the Young's modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neuttral surface). EStimate the critical height of a tree for a given radius of the trunk.
View Solution
