In some cases permittivity of substance turns out to be a complex or a negative quantity, and refractive index, respectively, a complex (n'=n+ix) or an imaginary (n'=ix) quantity. Write the equation of a plane wave for both of these cases and find out the physical meaning of such refractive indices.
Let us write the solutions of the wave equation in the form
A=A0ei(ωt−kx)
where k=2πλ and λ is the wavelength in the medium. If n'=n+iχ, then
k=2πλ0n'
(λ0 is the wavelength in vaccume) and the equation becomes
A=A0eχ'xexp (i(ωt1−k'x))
where χ'=2πλ0χ and k'=2πλ0n. In real form,
A=A0eχ'xcos(ωt−k'x)
This represents a plane wave whose amplitude diminished as it propagates to the right (privided χ'<0).
when n'=iχ, the similarly
A=A0eχ'xcosωt
(on putting n=0 in the above equation).
This represents a standing wave whose amplitude diminishes as one goes to the right (if χ'<0). The wavelength of the wave is infinite (k'=0).
Waves of the former type are realized inside metals as well as inside dielectrics when there is total reflection. (pentration of wave).
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources
22 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Thermal Equation
47 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Huygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
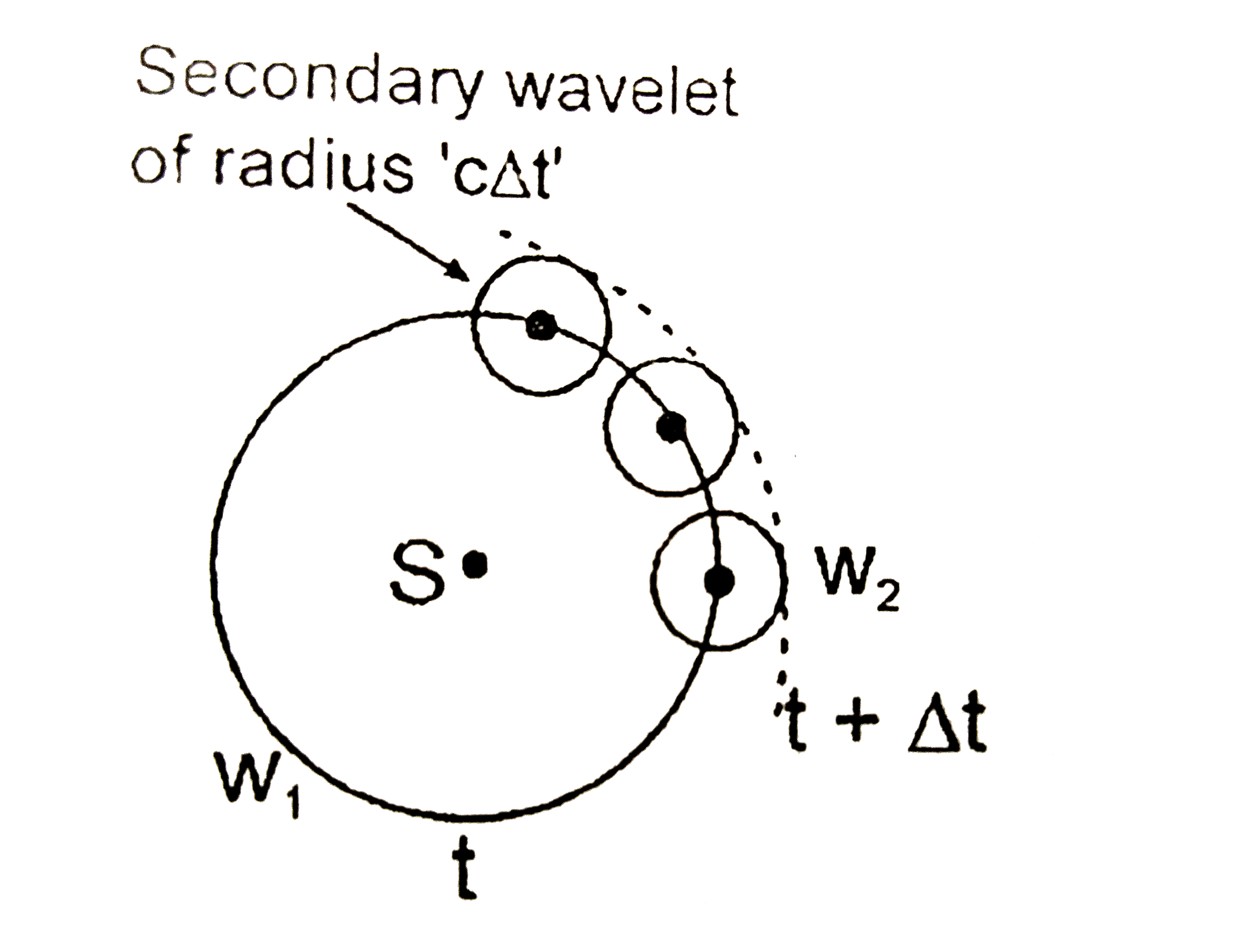
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View SolutionConsider two coherent sources S1andS2 producing monochromatic waves to produce interference patten. Let the displacement of the wave produced by S1 be given by
and the displacement by S2 be Y1=acosωt
Y2=acos(ωt−ϕ)
Find out expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
I=4a2cos2ϕ/2
Hence establish the conditions for constructive and destructive interference.
(b) What is the effect on the interference friinges in Young's double slit experiment when (i) the width of the source slit is increased, (ii) the monochromatic source is replaced by a source is replaced by a source of white light ?
OR
(a) A ray, 'PQ' of light on the face AB of glass prism ABC (as shown in the figure) and emerges out of the face AC. Trace the path of the ray. Show that
∠i+∠e=∠A+∠δ
Where δ and e denote the angle of deviation and angle of emergence respectively.
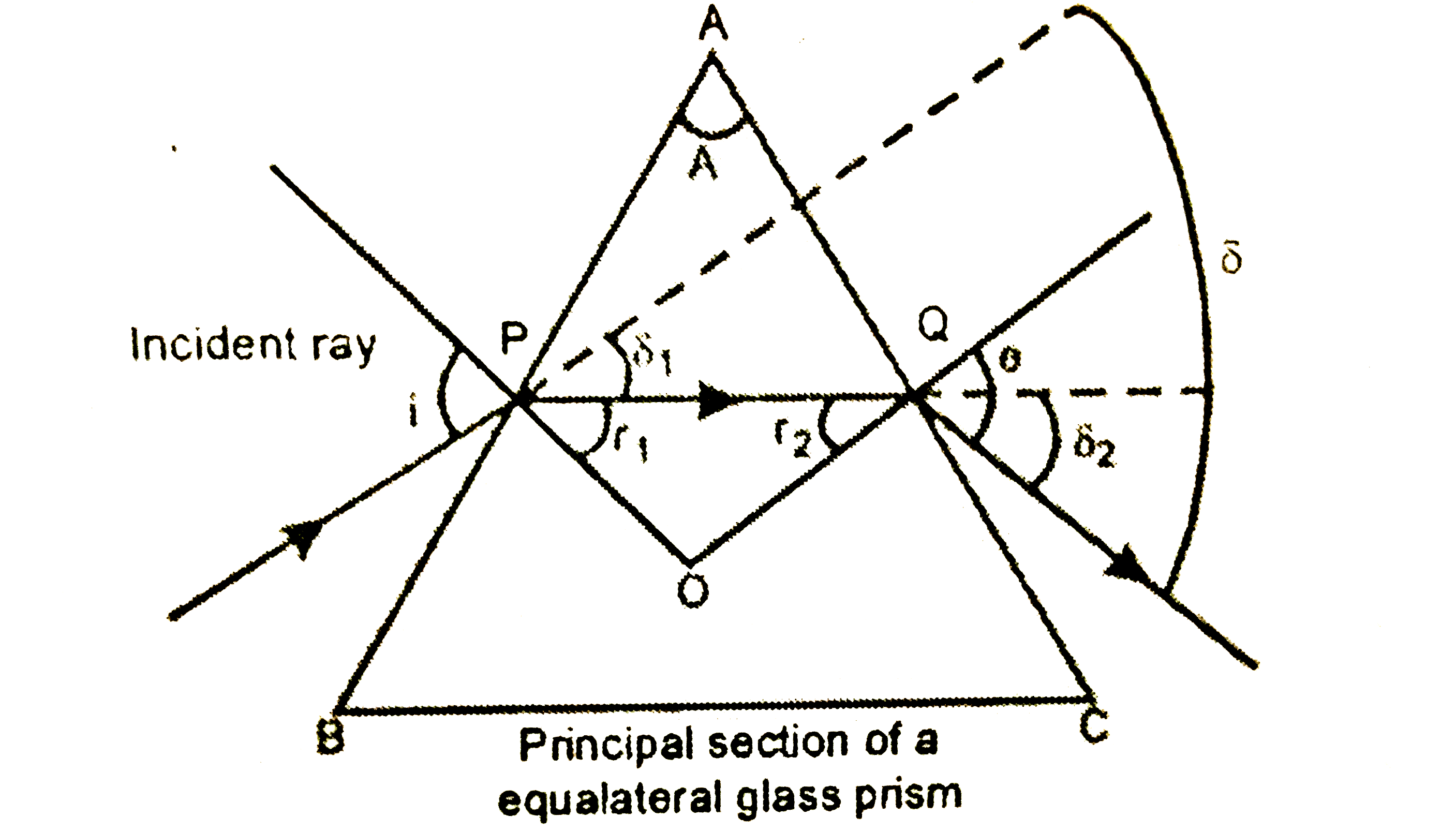
Plot a graph showing the variation of the angle of deviation as a function of angle of incidence. state the condition under which ∠δ is minimum.
(b) Find out the relation between the refractive index (μ) of the glass prism and ∠A for the case when the angle of prism (A) is equal to the angle of minimum deviation (δm) . Hence obtain the value of the refractive index for angle Ae=60∘ .
View Solution
Knowledge Check
_E01_074_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_074_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q. A point source of light is placed at origin, in air. the equation of wavefront of the wave at time t, emitted by source at t=0 is (take refractive index of air as 1)Ax+y+z=ctBx2+y2+z2=t2Cxy+yz+zx=c2t2Dx2+y2+z2=c2t2Huygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
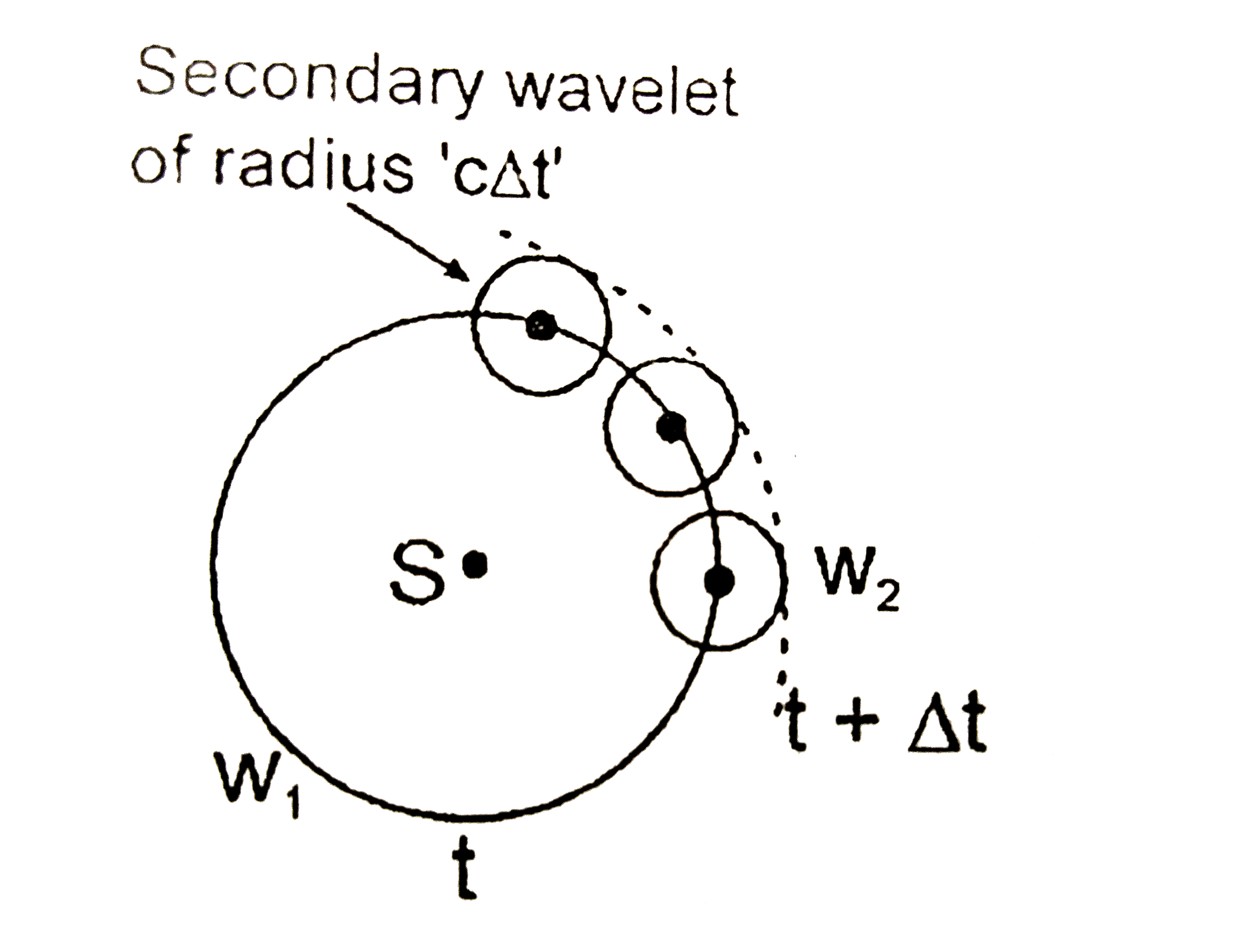
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)Ax+y+z=ctBx2+y2+z2=t2Cxy+yz+zx=c2t2Dx2+y2+z2=c2t2Most materials have the refractive index, n>1. So, when a light ray from air enters a naturally occuring material, then by Snell's law, sinθ1sinθ2=n1n2, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, n=(c/v)=±√εr,μr, where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium, εr and μr are negative, one must choose the negative root of n. Such negative refractive index materials can now be artifically prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
Answer the following questions :
Choose the correct statement.A B
B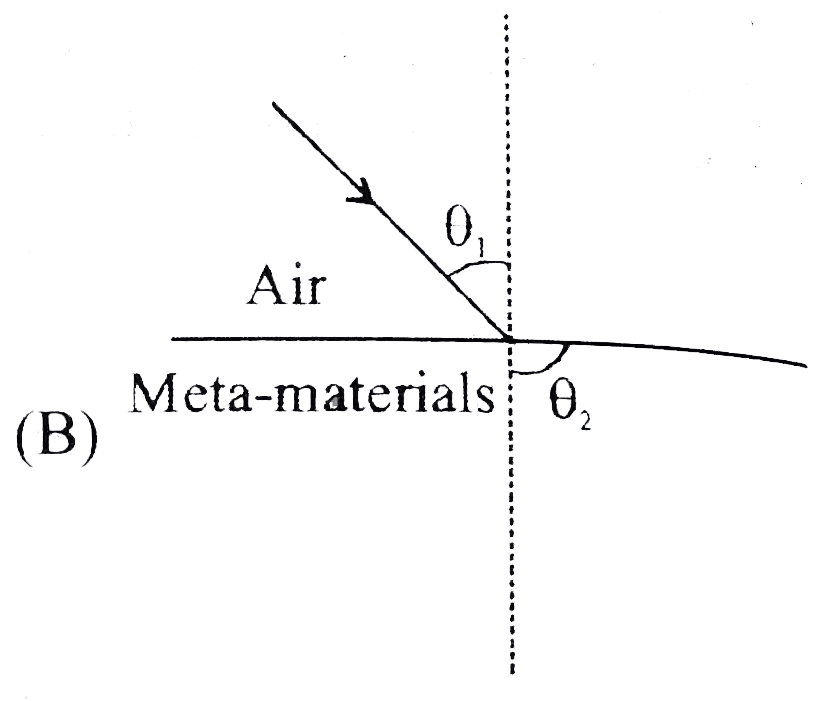 C
C D
D
An equiconvex lens of refractive index n, focal length/and radius of curvature R is immersed in a liquid medium of refractive index nm. For (?) nm>n, and (ii) nm<n, draw the ray diagrams in the two cases when a beam of light coming parallel to the principal axis is incident on the lens. Also find the focal length of the lens in terms of the original focal length and the refractive indices of the lens and that of the medium.
View SolutionAll questions refer to the diagram given below. The denoted lines represent the two surfaces of a lens that may be plane or curved. R1 and R2 are the radii of curvature of the surfaces on the left and right respectively. The refractive index of the medium to the left of the lens is n1, that of the material of the lens itself is n2, and that of the medium to the lens is n3. The first and second focal lengths of the lens are f1 and f2 respectively.
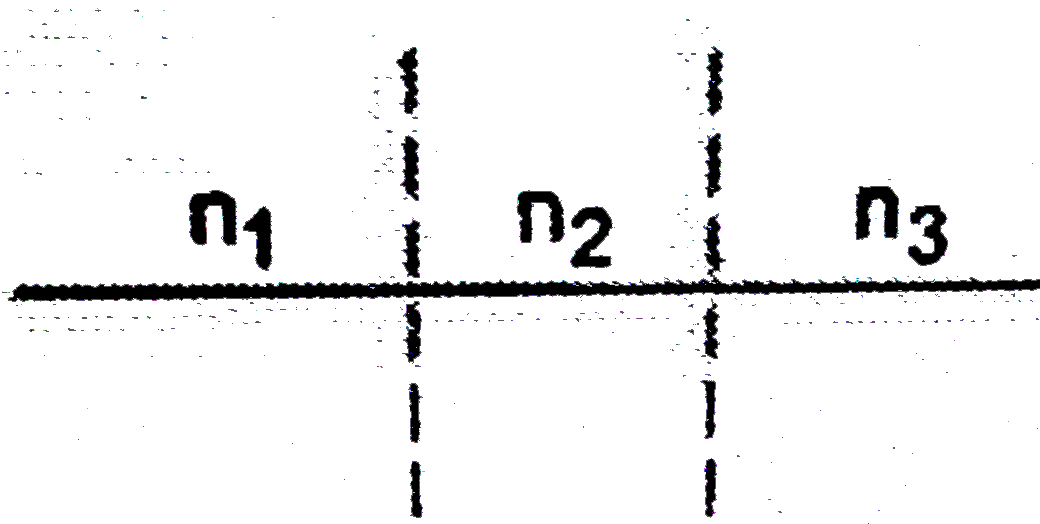
Column A contains certain conditions and column B contains some results which may follow from such conditions.
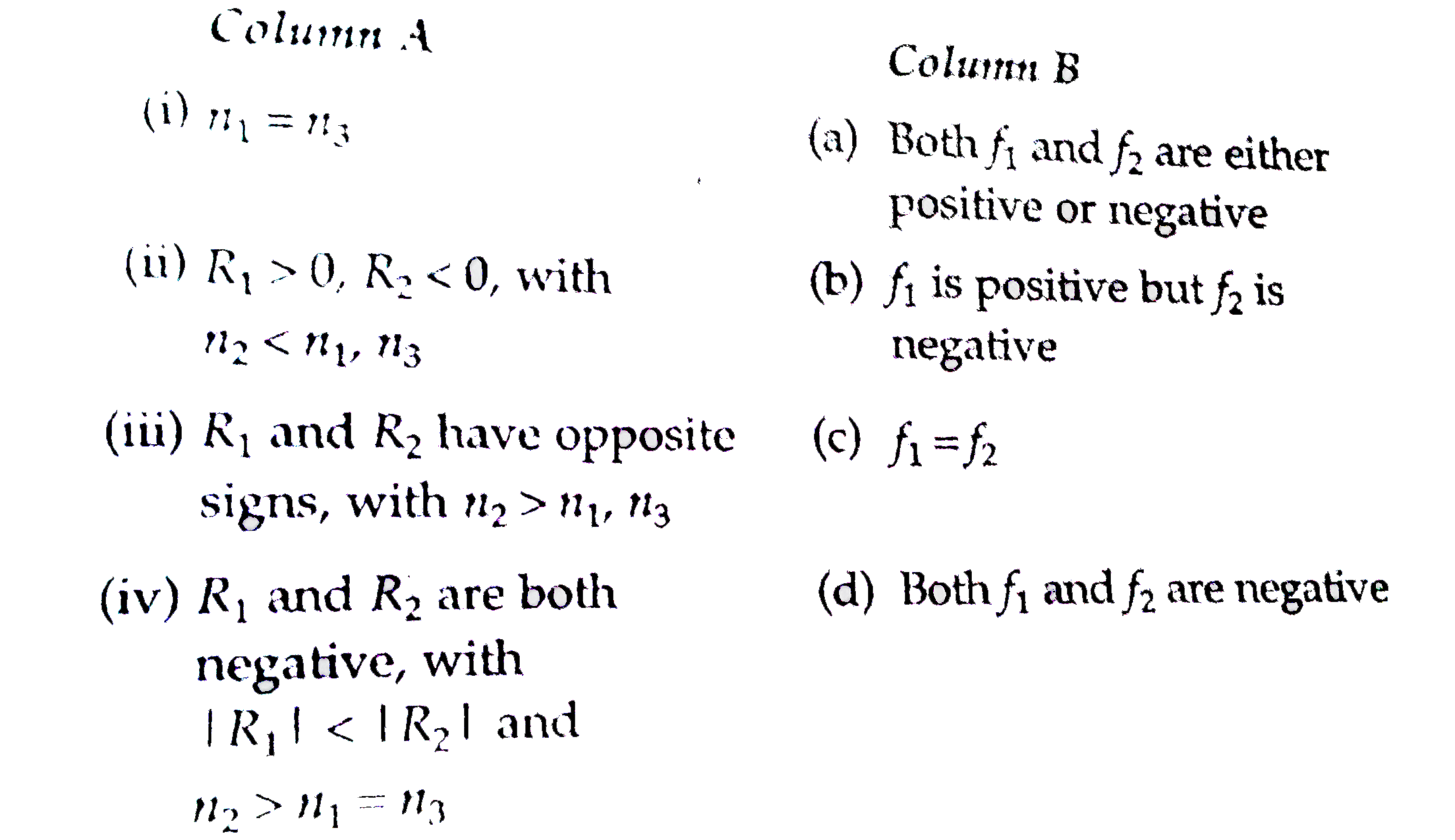
View SolutionTo decrease light losses due to reflection from the glass surface the latter is coated with a thin layer of substance whose refractive index n'=√n, where n is the refractive index of the glass. In this case the amplitudes of electromagnetic oscillations that coating is the glass reflectivity in the direction of the normal equal to zero for light with wavelength λ?
View SolutionA light wave falls normally on the surface of glass coated with a layer of transparent substance. Neglecting secondary reflections, demonstrate that the amplitudes of light waves reflected from the two surfaces of such a laver will be equal under the condition n'=√n, where n' and n are the refractive indiced of the layer and the glass respectively.
View SolutionMost materials have the refractive index, n>1. So, when a light ray from air enters a naturally occuring material, then by Snell's law, sinθ1sinθ2=n1n2, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, n=(c/v)=±√εr,μr, where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium, εr and μr are negative, one must choose the negative root of n. Such negative refractive index materials can now be artifically prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
Answer the following questions :
For light incident from air on a meta-material, the appropriate ray diagram is
View Solution
